Question

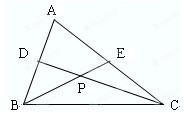如图，在△ABC中，AB=

2

3

AC，D、E分别为边AB、AC的中点，CD与BE相交于点P，
（1）若AB=2，四边形ADPE的面积记为S（A），试用角A表示出S（A），并求S的最大值；
（2）若

BE

CD

＜t恒成立，求t的最小值．

Answer 1

分析：（1）利用重心的性质和等底或等高的三角形的面积的比及三角函数的单调性即可得出；
（2）利用余弦定理和三角函数的单调性即可得出．

解答：解：（1）∵点P是△ABC的重心，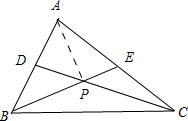
∴S=S_△APD+S_△AEP=

1

3

S△ABC=

1

6

AB•AC•sinA=

1

6

×2×3×sinA=sinA．
当A=

π

2

时，S取得最大值1．
（2）设AB=2x，AC=3x，

BE2

CD2

=

4x2+ 9x2 4 -2×2x× 3x 2 cosA

9x2+x2-2×x×3x×cosA

=

25-24cosA

40-24cosA

=1-

15

40-24cosA

，
∵A∈（0，π），∴cosA∈（-1，1），可得

1

4

＜

BE

CD

＜

7

8

，
若

BE

CD

＜t恒成立，则t≥

7

8

，
∴t的最小值为

7

8

．

点评：熟练掌握重心的性质、等底或等高的三角形的面积的比、三角函数的单调性、余弦定理是解题的关键．