题目内容
设ab<0,则方程y=ax+b和bx2+ay2=ab表示的曲线只能是( )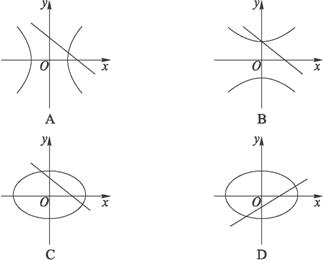
B
解析:bx2+ay2=ab变形为![]() =1,∴ab<0.∴对应图形为双曲线.
=1,∴ab<0.∴对应图形为双曲线.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
题目内容
设ab<0,则方程y=ax+b和bx2+ay2=ab表示的曲线只能是( )
B
解析:bx2+ay2=ab变形为![]() =1,∴ab<0.∴对应图形为双曲线.
=1,∴ab<0.∴对应图形为双曲线.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案