题目内容
已知向量 ,
,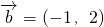 ,则向量
,则向量 与
与 的关系为
的关系为
- A.相等
- B.共线
- C.模相等
- D.垂直
B
分析:由已知中向量,表示出向量 与
与 的关系,结合向量平行(共线)的充要条件,判断它们的关系即可得到答案.
的关系,结合向量平行(共线)的充要条件,判断它们的关系即可得到答案.
解答:∵向量 ,
,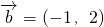 ,
,
∴ =(-2,
=(-2, ),
), =(4,-1)
=(4,-1)
∵(-2)•(-1)- •4=0
•4=0
∴向量 与
与 的关系为共线
的关系为共线
故选B.
点评:本题考查的知识点平面向量共线(平行)的坐标表示,其中根据向量平行(共线)的充要条件,得出向量 与
与 的关系,是解答本题的关键.
的关系,是解答本题的关键.
分析:由已知中向量,表示出向量
 与
与 的关系,结合向量平行(共线)的充要条件,判断它们的关系即可得到答案.
的关系,结合向量平行(共线)的充要条件,判断它们的关系即可得到答案.解答:∵向量
 ,
,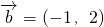 ,
,∴
 =(-2,
=(-2, ),
), =(4,-1)
=(4,-1)∵(-2)•(-1)-
 •4=0
•4=0∴向量
 与
与 的关系为共线
的关系为共线故选B.
点评:本题考查的知识点平面向量共线(平行)的坐标表示,其中根据向量平行(共线)的充要条件,得出向量
 与
与 的关系,是解答本题的关键.
的关系,是解答本题的关键. 
练习册系列答案
相关题目
 ,向量
,向量 ,向量
,向量 ,则向量
,则向量 与向量
与向量 的夹角的取值范围是( )
的夹角的取值范围是( ) B.
B. C.
C. D.
D.
 ,向量
,向量 ,向量
,向量 ,则向量
,则向量 与向量
与向量 的夹角的取值范围是( )
的夹角的取值范围是( ) B.
B. C.
C. D.
D.
 ,且
,且 ,则向量
,则向量 与
与 的夹角为(
)
的夹角为(
) B.
B. C.
C. D.
D.
 ,
, ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )

