题目内容
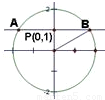 过点(0,1)的直线与圆x2+y2=4相交于A,B两点,则|AB|的最小值为( )
过点(0,1)的直线与圆x2+y2=4相交于A,B两点,则|AB|的最小值为( )A.2
B.
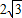
C.3
D.
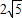
【答案】分析:计算弦心距,再求半弦长,得出结论.
解答:解:如图|AB|最小时,弦心距最大为1,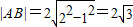 .
.
故选B.
点评:数形结合解答本题,它是选择题可以口算、心算、甚至不算,得出结果最好.
解答:解:如图|AB|最小时,弦心距最大为1,
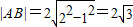 .
.故选B.
点评:数形结合解答本题,它是选择题可以口算、心算、甚至不算,得出结果最好.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目