Question

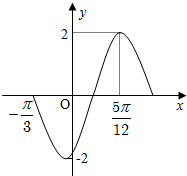函数f（x）=2sin（ωx+φ）（ω＞0，-

π

2

＜φ＜

π

2

）的部分图象如图所示，则f（0）的值是

 

．

Answer 1

分析：由函数的部分图象得到函数的周期，求出ω，代入(

5

12

π，2)求出φ值，则函数的解析式可求，取x=0得到f（0）的值．

解答：解：∵

3

4

T=

5π

12

-(-

π

3

)=

3

4

π，∴T=π，∴ω=2
把(

5

12

π，2)代入，得2sin(

5

6

π+φ)=2⇒

5

6

π+φ=

π

2

+2kπ，
∴φ=-

π

3

+2kπ，k∈Z，∵-

π

2

＜φ＜

π

2

，∴φ=-

π

3

，
∴f(x)=2sin(2x-

π

3

)．
则f(0)=2sin(-

π

3

)=-

3

．
故答案为-

3

．

点评：本题考查了由函数y=Asin（ωx+φ）的部分图象求函数解析式，关键是确定φ的值，是中档题．