题目内容
已知数列{an}中,a1=t,a2=t2(t>0且t≠1),若x=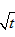 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记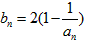 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有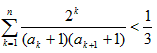 。
。
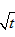 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记
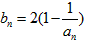 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;(Ⅲ)当t=2时,求证:对于任意的正整数n,有
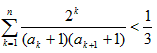 。
。 解:(Ⅰ) ,
,
由题意 ,即
,即 ,
,
∴ ,
,
∵t>0且t≠1,
∴数列 是以
是以 为首项,t为公比的等比数列,
为首项,t为公比的等比数列,
∴ ,
,
∴

以上各式两边分别相加得 ,
,
∴ ,
,
当n=1时,上式也成立,
∴ ;
;
(Ⅱ)当t=2时, ,
,
∴

由 ,得
,得 ,
, ,
,
当 时,
时, ,
,
当 时,
时, ,
,
因此n的最小值为1005;
(Ⅲ)∵ ,
,
∴ <
< 。
。
 ,
,由题意
 ,即
,即 ,
,∴
 ,
,∵t>0且t≠1,
∴数列
 是以
是以 为首项,t为公比的等比数列,
为首项,t为公比的等比数列, ∴
 ,
,∴


以上各式两边分别相加得
 ,
,∴
 ,
,当n=1时,上式也成立,
∴
 ;
;(Ⅱ)当t=2时,
 ,
,∴


由
 ,得
,得 ,
, ,
, 当
 时,
时, ,
,当
 时,
时, ,
,因此n的最小值为1005;
(Ⅲ)∵
 ,
,∴
 <
< 。
。
练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|