题目内容
(本小题12分)如图,甲船以每小时30 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
【答案】
乙船每小时航行30 海里
海里
【解析】
试题分析:如图所示,连结A1B2.

由已知A2B2=10 ,A1A2=30
,A1A2=30 ×
× =10
=10 ,
,
∴A1A2=A2B2.又∠A1A2B2=180°-120°=60°,
∴△A1A2B2是等边三角形,
∴A1B2=A1A2=10 .
.
由已知A1B1=20,∠B1A1B2=105°-60°=45°.
在△A1B2B1中,由余弦定理得

=202+(10 )2-2×20×10
)2-2×20×10 ×
×
=200,
∴B1B2=10 .
.
因此,乙船的速度为 ×60=30
×60=30 (海里/小时).
(海里/小时).
答:乙船每小时航行30 海里
海里
考点:解三角形的运用
点评:解决的关键是通过作图来得到对应的三角形,然后分析边和角,结合余弦定理来求解得到,属于基础题。

练习册系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面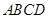 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在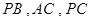 上,且
上,且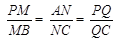
 ∥平面
∥平面 .
. 与平面面
与平面面
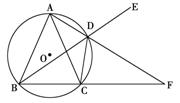

 平面BCD;
平面BCD;