题目内容
（本小题满分12分，（Ⅰ）小题5分，（Ⅱ）小题7分）
设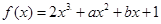
的导数为
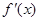，若函数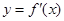
的图像关于直线
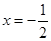对称，且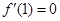
．
（Ⅰ）求实数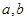
的值（Ⅱ）求函数
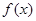的极值
【答案】
（I）由题设条件知
由于
（II）函数
处取得极大值
处取得极小值
【解析】(I)由于
是二次函数,根据其对称轴为
可求出a值,再利用
可求出b值.
(II)在(I)的基础上可以利用导数研究其极值即可.要注意极大值和极小值的判断方法,左正右负为极大,左负右正为极小.
解：（I）因
从而
即
关于直线
对称，从而由题设条件知
又由于…………5分
（II）由（I）知
令
当
上为增函数；
当
上为减函数；
当
上为增函数；
从而函数处取得极大值处取得极小值……12 分
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
