题目内容
四棱锥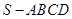 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面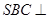 底面
底面 ,
, 为
为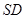 的中点,已知
的中点,已知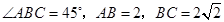 ,
,

(Ⅰ)求证: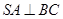 ;
;
(Ⅱ)在 上求一点
上求一点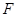 ,使
,使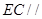 平面
平面 ;
;
(Ⅲ)求三棱锥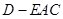 的体积.
的体积.
【答案】
(1)要证明线线垂直主要是通过线面垂直的性质定理来得到。
(2)根据题意,当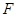 为
为 的中点
的中点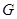 时,
时,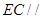 面
面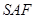 ,那么结合线面平行的判定定理来得到。
,那么结合线面平行的判定定理来得到。
(3)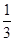
【解析】
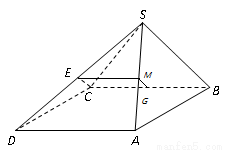
试题分析:(Ⅰ)证明:连接AC, 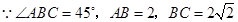 ,
,
由余弦定理得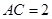 ,
,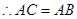 1分
1分
取 中点
中点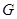 ,连接
,连接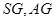 ,则
,则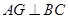 .
.
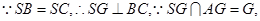
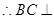 面
面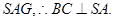 …………4分
…………4分
(Ⅱ)当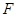 为
为 的中点
的中点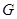 时,
时,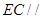 面
面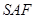 ……5分
……5分
证明:取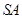 中点
中点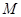 ,连接
,连接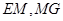 .
.
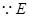 为
为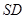 的中点,
的中点,
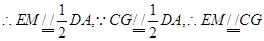
 四边形
四边形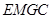 为平行四边形,
为平行四边形, .
7分
.
7分
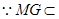 面
面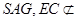 面
面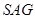 ,
,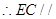 面
面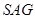 ,即
,即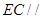 面
面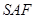 .
8分
.
8分
(Ⅲ)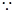 面
面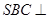 面
面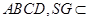 面
面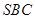 ,面
,面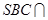 面
面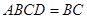 ,
,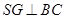 ,
,
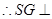 面
面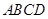 ,且
,且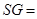 1,
1,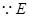 为
为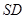 的中点,
的中点, 到面
到面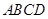 的距离为
的距离为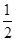 .
10分
.
10分
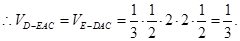 12分
12分
考点:空间线面关系,体积计算
点评:本小题主要考查空间线面关系、体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目
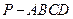 中,底面
中,底面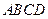 为平行四边形,
为平行四边形,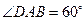 ,
,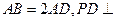 底面
底面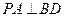 ;
;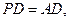 求二面角
求二面角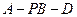 的余弦值.
的余弦值.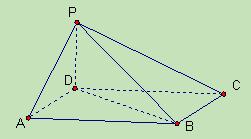
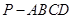 中,底面
中,底面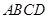 为平行四边形
为平行四边形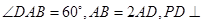 底面
底面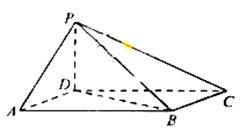
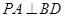
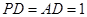 ,求棱锥
,求棱锥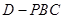 的高.
的高. 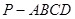 中,底面
中,底面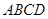 为平行四边形,
为平行四边形,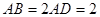 ,
,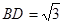 ,
,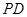 ⊥底面
⊥底面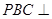 平面
平面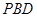 ;
;
 为
为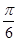 ,求
,求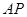 与平面
与平面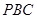 所成角的正弦值。
所成角的正弦值。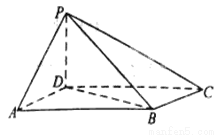
 中,底面
中,底面 为平行四边形,
为平行四边形, 底面
底面 ,
, ,
, ,
, ,E在棱
,E在棱 上, (Ⅰ) 当
上, (Ⅰ) 当 时,求证:
时,求证: 平面
平面 ; (Ⅱ)
当二面角
; (Ⅱ)
当二面角 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
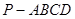 中,底面
中,底面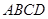 为平行四边形,
为平行四边形,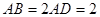 ,
,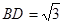 ,
,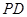 ⊥底面
⊥底面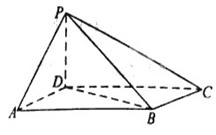
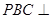 平面
平面 ;
;
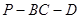 为
为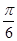 ,求
,求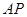 与平面
与平面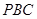 所成角的正弦值。
所成角的正弦值。