题目内容
(08年辽宁卷理)设函数![]() .
.
⑴求![]() 的单调区间和极值;
的单调区间和极值;
⑵是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
说明:本小题主要考查函数的导数,单调性,极值,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.满分14分.
解析:(Ⅰ)![]() .?????????????????????????? 2分
.?????????????????????????? 2分
故当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.??????????????????????????????????????????? 4分
单调递减.??????????????????????????????????????????? 4分
由此知![]() 在
在![]() 的极大值为
的极大值为![]() ,没有极小值.????????????????????????????? 6分
,没有极小值.????????????????????????????? 6分
(Ⅱ)()当![]() 时,
时,
由于![]() ,
,
故关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .????????????????????????????????????????????? 10分
.????????????????????????????????????????????? 10分
()当![]() 时,由
时,由![]() 知
知![]() ,其中
,其中![]() 为正整数,且有
为正整数,且有
![]() .????????????????????????????????????? 12分
.????????????????????????????????????? 12分
又![]() 时,
时,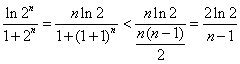 .
.
且![]() .
.
取整数![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,
,
则![]() ,
,
即当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集不是
的解集不是![]() .
.
综合()()知,存在![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,且
,且![]() 的取值范围为
的取值范围为![]() . 14分
. 14分

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目