题目内容
(1)已知a,b是正常数,a≠b,x,y∈(0,+∞),求证:
+
≥
,指出等号成立的条件;
(2)利用(1)的结论求函数f(x)=
+
(x∈(0,
))的最小值,指出取最小值时x的值.
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
(2)利用(1)的结论求函数f(x)=
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
(1)应用二元均值不等式,得(
+
)(x+y)=a2+b2+a2
+b2
≥a2+b2+2
=(a+b)2,
故
+
≥
.
当且仅当a2
=b2
,即
=
时上式取等号.
(2)由(1)f(x)=
+
≥
=25.
当且仅当
=
,即x=
时上式取最小值,即[f(x)]min=25.
| a2 |
| x |
| b2 |
| y |
| y |
| x |
| x |
| y |
a2
|
故
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
当且仅当a2
| y |
| x |
| x |
| y |
| a |
| x |
| b |
| y |
(2)由(1)f(x)=
| 22 |
| 2x |
| 32 |
| 1-2x |
| (2+3)2 |
| 2x+(1-2x) |
当且仅当
| 2 |
| 2x |
| 3 |
| 1-2x |
| 1 |
| 5 |

练习册系列答案
相关题目
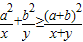 ,指出等号成立的条件;
,指出等号成立的条件;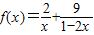 (
(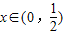 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.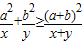 ,指出等号成立的条件;
,指出等号成立的条件;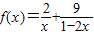 (
(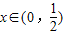 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.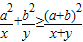 ,指出等号成立的条件;
,指出等号成立的条件;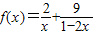 (
(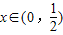 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.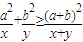 ,指出等号成立的条件;
,指出等号成立的条件;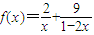 (
(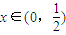 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.