题目内容
已知函数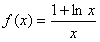 ,
,
(Ⅰ)设a>0,若函数在区间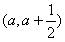 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(Ⅱ)如果当x≥1时,不等式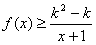 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
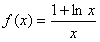 ,
,(Ⅰ)设a>0,若函数在区间
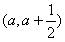 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;(Ⅱ)如果当x≥1时,不等式
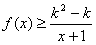 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。解:(Ⅰ)因为f(x)= ,
,
则f′(x)= ,x>0,
,x>0,
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以函数f(x)在x=1处取得极大值,
因为函数f(x)在区间 (其中a>0)上存在极值,
(其中a>0)上存在极值,
所以 ,解得
,解得 ;
;
(Ⅱ)不等式 ,即为
,即为 ,
,
记 ,
,
所以g′(x) ,
,
令h(x)=x-lnx,则h′(x)= ,
,
∵x≥1,
∴h′(x)≥0,
∴h(x)在[1,+∞)上单调递增,
∴h(x)min=h(1)=1>0,从而g′(x)>0,
故g(x)在[1,+∞)上也单调递增,
所以g(x)min=g(1)=2,
所以k2-k≤2,解得-1≤k≤2。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
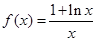 .
.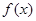 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;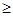 1时,不等式
1时,不等式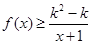 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.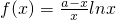 .
.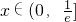 ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围.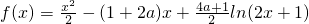 .
. .
. .
.