Question

设函数f(x)=sin(2x+φ)(-π＜φ＜0),y=f(x)图像的一条对称轴是直线x=.

(1)求φ;

(2)求函数y=f(x)的单调增区间;

(3)画出函数y=f(x)在区间［0,π］上的图像.

Answer 1

解:(1)∵x=是函数y=f(x)的图像的对称轴,

∴sin(2×+φ)=±1,∴+φ=kπ+,k∈Z,

∵-π＜φ＜0,∴φ=-.

(2)由(1)知φ=-,因此y=sin(2x-).

由题意,得2kπ-≤2x-≤2kπ+,k∈Z,

kπ+≤x≤kπ+,k∈Z,

∴函数y=sin(2x-)的单调增区间为［kπ+,kπ+］,k∈Z.

(3)由y=sin(2x-)知

x	0					π
y	-	-1	0	1	0	-

故函数y=f(x)在区间［0,π］上的图像如图1.

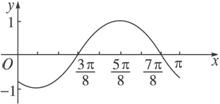
图1