题目内容
已知椭圆与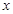 轴相切,左、右两个焦点分别为
轴相切,左、右两个焦点分别为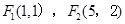 ,则原点O到其左准线的距离为 .
,则原点O到其左准线的距离为 .
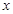 轴相切,左、右两个焦点分别为
轴相切,左、右两个焦点分别为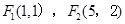 ,则原点O到其左准线的距离为 .
,则原点O到其左准线的距离为 .
试题分析:这一题已经超过江苏高考数学要求,同学们权当闲聊观赏.由于本题椭圆不是标准方程,我们只能根据椭圆的定义来解题.
 ,所以椭圆短轴所在直线方程为
,所以椭圆短轴所在直线方程为 ,即
,即 ,原点
,原点 到短轴所在直线的距离为
到短轴所在直线的距离为 .由椭圆(实际上是所有圆锥曲线)的光学性质:从一焦点发出的光线经过椭圆反射后(或反射延长线)通过另一个焦点,本题中切线是
.由椭圆(实际上是所有圆锥曲线)的光学性质:从一焦点发出的光线经过椭圆反射后(或反射延长线)通过另一个焦点,本题中切线是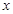 轴,设切点为
轴,设切点为 ,则
,则 ,于是
,于是 ,解得
,解得 ,因此
,因此 ,
, ,又
,又 ,
, ,所以
,所以 ,因此原点到左准线的距离应该是
,因此原点到左准线的距离应该是
 .
.
练习册系列答案
相关题目
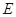 :
: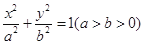 的左焦点为
的左焦点为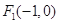 ,且过点
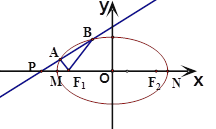
,且过点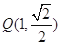 .
.
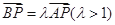 .
.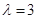 ,求
,求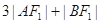 的值;
的值;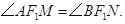




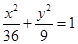 的弦被点
的弦被点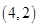 平分,则此弦所在直线的斜率为
平分,则此弦所在直线的斜率为  的焦点到直线
的焦点到直线 的距离为 .
的距离为 .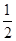 B.最小值
B.最小值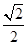 D.最小值
D.最小值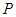 到两个焦点之间距离的和为
到两个焦点之间距离的和为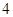 ,其中一个焦点的坐标为
,其中一个焦点的坐标为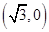 ,则椭圆的离心率为 .
,则椭圆的离心率为 .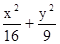 =1上任意一点,则点P到直线AB距离的最大值是______________.
=1上任意一点,则点P到直线AB距离的最大值是______________.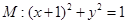 ,圆
,圆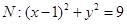 ,动圆
,动圆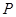 与圆
与圆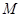 外切并且与圆
外切并且与圆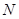 内切,圆心
内切,圆心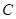 。
。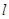 是与圆
是与圆 ,
,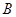 两点,当圆
两点,当圆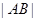 。
。