题目内容

椭圆C：
x2
4
+y2=1与动直线l：2mx-2y-2m+1=0（m∈R），则直线l与椭圆C交点的个数为（　　）
A．0B．1C．2D．不确定
整理直线方程得2m（x-1）+1-2y=0，
∴直线恒过（1，
1
2
）点，
把点（1，
1
2
）代入椭圆方程求得
12
4
+(
1
2
)2＜1，可知此点在椭圆的内部，
∴过此点的直线与椭圆有两个交点
故选C．
练习册系列答案
相关题目
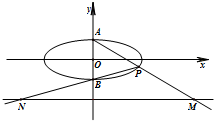在平面直角坐标系xOy中，如图，已知椭圆C：
x24
+y2=1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N；
（I）设直线AP、BP的斜率分别为k1，k2求证：k1•k2为定值；
（Ⅱ）求线段MN长的最小值；
（Ⅲ）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．
已知椭圆C：
x24
+y2=1，直线l与椭圆C相交于A、B两点，若以AB为直径的圆经过坐标原点．
（1）试探究：点O到直线AB的距离是否为定值，若是，求出该定值；若不是，请说明理由；
（2）求△AOB面积S的最小值．
已知椭圆C：
x2
4
+y2=1，左右焦点分别为F1，F2，
（1）若C上一点P满足∠F1PF2=90°，求△F1PF2的面积；
（2）直线l交C于点A，B，线段AB的中点为(1，
1
2
)，求直线l的方程．
（2013•沈阳二模）椭圆C：
x2
4
+y2=1与动直线l：2mx-2y-2m+1=0（m∈R），则直线l与椭圆C交点的个数为（　　）
（2008•普陀区二模）已知点E，F的坐标分别是（-2，0）、（2，0），直线EP，FP相交于点P，且它们的斜率之积为-
1
4
．
（1）求证：点P的轨迹在椭圆C：
x2
4
+y2=1上；
（2）设过原点O的直线AB交（1）题中的椭圆C于点A、B，定点M的坐标为(1，
1
2
)，试求△MAB面积的最大值，并求此时直线AB的斜率kAB；
（3）某同学由（2）题结论为特例作推广，得到如下猜想：
设点M（a，b）（ab≠0）为椭圆C：
x2
4
+y2=1内一点，过椭圆C中心的直线AB与椭圆分别交于A、B两点．则当且仅当kOM=-kAB时，△MAB的面积取得最大值．
问：此猜想是否正确？若正确，试证明之；若不正确，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网