题目内容
(本题满分12分)
已知等差数列{ },公差
},公差 ,
, ,且
,且 成等比数列.
成等比数列.
(I)求{ }的通项公式;
}的通项公式;
(II)设 ,求证:
,求证: .
.
(I) ;(II)详见解析.
;(II)详见解析.
【解析】
试题分析:(I)将已知条件转化为关于 的方程组,可求得
的方程组,可求得 .也可以先根据等差中项由
.也可以先根据等差中项由 先求
先求 ,再讲
,再讲 用
用 和公差
和公差 表示,根据等比中项列式求公差
表示,根据等比中项列式求公差 .根据等差的通项公式求
.根据等差的通项公式求 .(II)用错位相减法求
.(II)用错位相减法求 的前
的前 项和.再与2比较大小.
项和.再与2比较大小.
试题解析:【解析】
(I)由 得
得
因为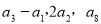 成等比数列,所以
成等比数列,所以 ,解得
,解得
所以 5分
5分
(II)设 ,令
,令 ①
①
所以 ②
②
① ②得: 8分
8分
所以 11分
11分
 12分
12分
考点:1等差的通项公式;2错位相减法求数列前 项和.
项和.

练习册系列答案
相关题目
 ,经过
,经过 天后体积与天数
天后体积与天数 的关系式为:
的关系式为: ,若新丸经过50天后,体积变为
,若新丸经过50天后,体积变为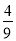
 ;若一个新丸体积变为
;若一个新丸体积变为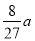 ,则需经过的天数为
,则需经过的天数为 的前
的前 项和
项和 当首项
当首项 和公差
和公差 变化时,若
变化时,若 是一个定值,则下列各数中为定值的是( )
是一个定值,则下列各数中为定值的是( )  B.
B. C.
C. D.
D.
 (y≠0) (B)
(y≠0) (B) (y≠0)
(y≠0) (y≠0) (D)
(y≠0) (D) (y≠0)
(y≠0) 满足
满足 ,下列选项中一定成立的是( )
,下列选项中一定成立的是( ) (B)
(B) (C)
(C) (D)
(D) 
 中,
中, 分别是角
分别是角 的对边,且满足
的对边,且满足 ,那么
,那么 (
( )为奇函数,
)为奇函数, ,
, ,则
,则
 D.5
D.5 ,
, 分别是R上的奇函数,偶函数,且满足
分别是R上的奇函数,偶函数,且满足 ,则有
,则有 B.
B.
 D.
D.