Question

正四棱台上、下底面的边长为b、a（a＞b）且侧面积等于两底面面积之和，则棱台的高是________．

Answer 1

分析：设A、B分别是棱台的底面中心，C、D分别为底面正方形边的中点．作出直角梯形ABCD如图，过C作CE⊥AD于E，设棱台的高为h，斜高为h'，据题意可得（4a+4b）h'=a²+b²，得h'=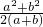，再在Rt△CDE中，利用勾股定理可得CE=，即得即棱台的高h的大小．
解答：设棱台的高为h，斜高为h'，设A、B分别是棱台的底面中心，C、D分别为底面正方形边的中点
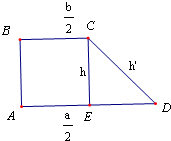
作出直角梯形ABCD如图，过C作CE⊥AD于E
∵棱台的侧面积等于两底面面积之和，
∴（4a+4b）h'=a²+b²，得h'=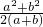
Rt△CDE中，DE=AD-BC=（a-b）
∴CE===
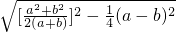即棱台的高h=
故答案为：
点评：本题给出棱台的侧面积等于上下底面之和，求棱台的高．着重考查了勾股定理、正棱台的基本概念和性质等知识，属于基础题．