题目内容
(1)已知2x≤( )x-3,求函数y=(
)x-3,求函数y=( )x的值域.
)x的值域.
(2)函数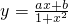 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且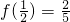 ,求函数f(x)的解析式.
,求函数f(x)的解析式.
解:(1)∵2x≤( )x-3=26-2x
)x-3=26-2x
由函数y=2x为定义在R的增函数
故x≤6-2x
解得x≤2
又∵函数y=( )x为定义在R的减函数
)x为定义在R的减函数
∴当x=2时,函数取最小值 ,无最大值
,无最大值
故函数y=( )x的值域为[
)x的值域为[ ,+∞)
,+∞)
(2)∵函数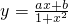 是定义在(-1,1)上的奇函数,
是定义在(-1,1)上的奇函数,
∴f(0)=0,即b=0
又∵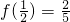 ,即
,即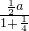 =
=
解得a=1
∴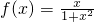
分析:(1)根据对数函数的单调性,解不等式2x≤( )x-3,求出x的范围(定义域),进而根据指数函数的图象和性质,可得函数y=(
)x-3,求出x的范围(定义域),进而根据指数函数的图象和性质,可得函数y=( )x的值域.
)x的值域.
(2)若函数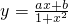 是定义在(-1,1)上的奇函数,可得f(0)=0,结合
是定义在(-1,1)上的奇函数,可得f(0)=0,结合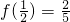 ,构造关于a,b的方程组,解方程组,可得答案.
,构造关于a,b的方程组,解方程组,可得答案.
点评:本题考查的知识点是指数函数的图象和性质,函数的值域,函数解析式的求法,函数的奇偶性,是函数图象和性质的简单综合应用.
 )x-3=26-2x
)x-3=26-2x由函数y=2x为定义在R的增函数
故x≤6-2x
解得x≤2
又∵函数y=(
 )x为定义在R的减函数
)x为定义在R的减函数∴当x=2时,函数取最小值
 ,无最大值
,无最大值故函数y=(
 )x的值域为[
)x的值域为[ ,+∞)
,+∞)(2)∵函数
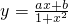 是定义在(-1,1)上的奇函数,
是定义在(-1,1)上的奇函数,∴f(0)=0,即b=0
又∵
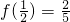 ,即
,即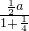 =
=
解得a=1
∴
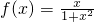
分析:(1)根据对数函数的单调性,解不等式2x≤(
 )x-3,求出x的范围(定义域),进而根据指数函数的图象和性质,可得函数y=(
)x-3,求出x的范围(定义域),进而根据指数函数的图象和性质,可得函数y=( )x的值域.
)x的值域.(2)若函数
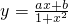 是定义在(-1,1)上的奇函数,可得f(0)=0,结合
是定义在(-1,1)上的奇函数,可得f(0)=0,结合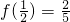 ,构造关于a,b的方程组,解方程组,可得答案.
,构造关于a,b的方程组,解方程组,可得答案.点评:本题考查的知识点是指数函数的图象和性质,函数的值域,函数解析式的求法,函数的奇偶性,是函数图象和性质的简单综合应用.

练习册系列答案
相关题目