题目内容
已知函数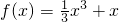 ,x∈R,如果至少存在一个实数x,使f (a-x)+f (ax2-1)<0,成立,则实数a的取值范围为
,x∈R,如果至少存在一个实数x,使f (a-x)+f (ax2-1)<0,成立,则实数a的取值范围为
- A.(
 ,+∞)
,+∞) - B.(-2,
 ]
] - C.(-∞,
 )
) - D.(1,
 )∪(-
)∪(- ,-1)
,-1)
C
分析:先判断出f(x)是增函数,且为奇函数.由已知,得出ax2-x+a-1<0有解.考虑其否定:对于任意的实数x,都有ax2-x+a-1≥0”,再求出实数a的取值范围.
解答:由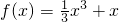 ,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数.
,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数.
将f (a-x)+f (ax2-1)<0,化为f (a-x)<-f (ax2-1),即f (a-x)<f (-ax2+1),得出a-x<-ax2+1,
整理ax2-x+a-1<0.①
由已知,不等式①有解,其否定为“对于任意的实数x,都有ax2-x+a-1≥0”,此时须 ,解得a≥
,解得a≥ .
.
所以实数a的取值范围为(-∞, ).
).
故选C.
点评:本题考查不等式求解,函数的性质.化抽象为具体,正难则反,间接求解.是好题.
分析:先判断出f(x)是增函数,且为奇函数.由已知,得出ax2-x+a-1<0有解.考虑其否定:对于任意的实数x,都有ax2-x+a-1≥0”,再求出实数a的取值范围.
解答:由
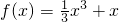 ,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数.
,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数.将f (a-x)+f (ax2-1)<0,化为f (a-x)<-f (ax2-1),即f (a-x)<f (-ax2+1),得出a-x<-ax2+1,
整理ax2-x+a-1<0.①
由已知,不等式①有解,其否定为“对于任意的实数x,都有ax2-x+a-1≥0”,此时须
 ,解得a≥
,解得a≥ .
.所以实数a的取值范围为(-∞,
 ).
).故选C.
点评:本题考查不等式求解,函数的性质.化抽象为具体,正难则反,间接求解.是好题.

练习册系列答案
相关题目
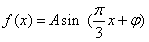 ,x∈R,A>0,
,x∈R,A>0,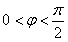 。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。
。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。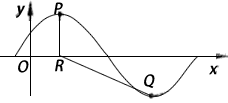
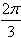 ,求A的值。
,求A的值。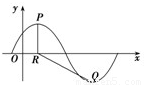 已知函数
已知函数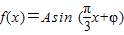 ,x∈R,A>0,
,x∈R,A>0,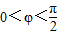 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).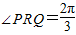 ,求A的值.
,求A的值.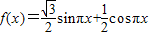 ,x∈R.
,x∈R.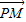 与
与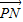 的夹角的余弦.
的夹角的余弦.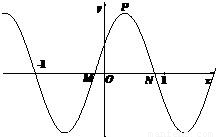
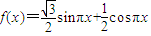 ,x∈R.
,x∈R.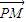 与
与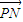 的夹角的余弦.
的夹角的余弦.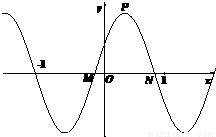
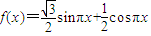 ,x∈R.
,x∈R.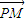 与
与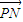 的夹角的余弦.
的夹角的余弦.