题目内容
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,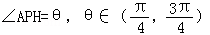 .
.
(1)求l关于θ的函数关系式;
(2)定义比值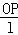 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: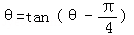 时,招贴画最优美.
时,招贴画最优美.
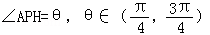 .
.(1)求l关于θ的函数关系式;
(2)定义比值
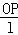 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: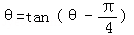 时,招贴画最优美.
时,招贴画最优美.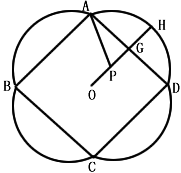
解:(1)当θ∈ 时,点P在线段OG上,AP=
时,点P在线段OG上,AP= ;
;
当θ∈ 时,点P在线段GH上,AP=
时,点P在线段GH上,AP= ;
;
当θ= 时,AP=a.
时,AP=a.
综上所述AP= ,θ∈
,θ∈ ,
,
所以,弧AD的长L= .
.
故所求函数关系式为L= ,θ∈
,θ∈ .
.
(2)证明:当θ∈( ,
, )时,OP=OG﹣PG=a﹣
)时,OP=OG﹣PG=a﹣ ;
;
当θ∈ 时,OP=OG+GH=a+
时,OP=OG+GH=a+ ;
;
当θ= 时,OP=a.
时,OP=a.
所以,OP=a﹣ ,θ∈
,θ∈ .
.
从而, ,θ∈
,θ∈ .
.

所以:当θ满足θ=tan(θ﹣ )时,函数f(θ)即
)时,函数f(θ)即 取得最大值,此时招贴画最优美.
取得最大值,此时招贴画最优美.
 时,点P在线段OG上,AP=
时,点P在线段OG上,AP= ;
;当θ∈
 时,点P在线段GH上,AP=
时,点P在线段GH上,AP= ;
;当θ=
 时,AP=a.
时,AP=a.综上所述AP=
 ,θ∈
,θ∈ ,
,所以,弧AD的长L=
 .
.故所求函数关系式为L=
 ,θ∈
,θ∈ .
.(2)证明:当θ∈(
 ,
, )时,OP=OG﹣PG=a﹣
)时,OP=OG﹣PG=a﹣ ;
;当θ∈
 时,OP=OG+GH=a+
时,OP=OG+GH=a+ ;
;当θ=
 时,OP=a.
时,OP=a.所以,OP=a﹣
 ,θ∈
,θ∈ .
.从而,
 ,θ∈
,θ∈ .
.
所以:当θ满足θ=tan(θ﹣
 )时,函数f(θ)即
)时,函数f(θ)即 取得最大值,此时招贴画最优美.
取得最大值,此时招贴画最优美.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,
 .(1)求l关于θ的函数关系式;(2)定义比值
.(1)求l关于θ的函数关系式;(2)定义比值 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: 时,招贴画最优美.
时,招贴画最优美.