题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 同时满足:①对任意
同时满足:①对任意![]() ,都有
,都有![]() ;②当
;②当![]() 时,
时,![]() ,
,
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)若关于![]() 的方程
的方程![]() 在
在![]() 上有实数解,求实数
上有实数解,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,关于
,关于![]() 的不等式
的不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)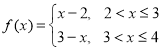 ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)由①求函数周期T=2,然后由函数周期性和递推关系式求出![]() 的函数解析式;
的函数解析式;
(2)设方程的实数解为![]() ,利用(1)的结论解方程和不等式
,利用(1)的结论解方程和不等式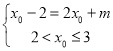 或
或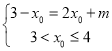 即可求出参数
即可求出参数![]() 的取值范围;
的取值范围;
(3)先求函数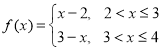 的最小值
的最小值![]() ,再由函数的周期性可得在
,再由函数的周期性可得在![]() 上恒有
上恒有![]() ,然后求得在
,然后求得在![]() 上
上![]() 的最大值为
的最大值为![]() 最后由
最后由![]() 即可得出答案.
即可得出答案.
(1)∵对任意![]() ,都有
,都有![]() ,∴
,∴![]() ,
,
即![]() 则可得函数的周期为T=2,
则可得函数的周期为T=2,
当![]() 时,
时,![]() ,∴当
,∴当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() 时,
时,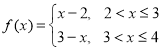 ;
;
(2)设关于![]() 的方程
的方程![]() 在
在![]() 上的实数解为
上的实数解为![]()
则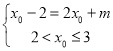 或
或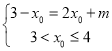 ,∴
,∴ 或
或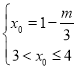
∴![]() 或
或![]()
(3)由(1)得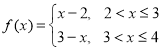 可得在
可得在![]() 上
上![]() ,又因函数
,又因函数![]() 的周期为T=2,则可得
的周期为T=2,则可得![]() 上恒有
上恒有![]() ,
,
令函数![]() 得在
得在![]() 上单调递增,则可得
上单调递增,则可得![]() ,
,
由题意对任意![]() ,关于
,关于![]() 的不等式
的不等式![]() 都成立,
都成立,
则可得恒有:![]() 即
即![]() 解得
解得![]() .
.

练习册系列答案
相关题目