题目内容
当 时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题:
时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题:
①函数y=f(x)的值域为[0, ];
];
②函数y=f(x)的图象关于直线x= (k∈Z)对称;
(k∈Z)对称;
③函数y=f(x)是周期函数,且最小正周期为1;
④函数y=f(x)在[- ,
, ]上是增函数.
]上是增函数.
其中正确的命题的序号是________.
①②③
分析:本选择题可利用特殊值加以解决.因为m为整数,故函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值即f(x)=|=|x-m|,可取m为几个特殊的整数对选项一一进行研究.
解答: 解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值,
解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值,
即f(x)=|x-m|,
取m=0时,- <x≤
<x≤ ,f(x)=|x|,
,f(x)=|x|,
取m=1时,1- <x≤1+
<x≤1+ ,f(x)=|x-1|,
,f(x)=|x-1|,
取m=2时,2- <x≤2+
<x≤2+ ,f(x)=|x-2|,分别作出它们的图象,如图所示.
,f(x)=|x-2|,分别作出它们的图象,如图所示.
由图象可知正确命题为①②③,
故答案为:①②③.
点评:本小题主要考查函数单调性的应用、函数对称性的应用、函数的图象等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:本选择题可利用特殊值加以解决.因为m为整数,故函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值即f(x)=|=|x-m|,可取m为几个特殊的整数对选项一一进行研究.
解答:
 解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值,
解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值,即f(x)=|x-m|,
取m=0时,-
 <x≤
<x≤ ,f(x)=|x|,
,f(x)=|x|,取m=1时,1-
 <x≤1+
<x≤1+ ,f(x)=|x-1|,
,f(x)=|x-1|,取m=2时,2-
 <x≤2+
<x≤2+ ,f(x)=|x-2|,分别作出它们的图象,如图所示.
,f(x)=|x-2|,分别作出它们的图象,如图所示.由图象可知正确命题为①②③,
故答案为:①②③.
点评:本小题主要考查函数单调性的应用、函数对称性的应用、函数的图象等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
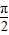 )的最高点D的坐标为(
)的最高点D的坐标为(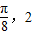 ),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(
),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(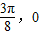 );
);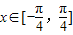 时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.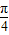 个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.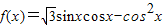 .
.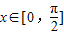 时,求函数f(x)的最大值和最小值.
时,求函数f(x)的最大值和最小值. 时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题:
时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题: ];
]; (k∈Z)对称;
(k∈Z)对称; ,
, ]上是增函数.
]上是增函数.