题目内容
已知椭圆的中心在原点,焦点在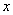 轴上,离心率为
轴上,离心率为 ,过椭圆上一点
,过椭圆上一点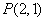 作倾斜角互补的两条直线,分别交椭圆于不同两点
作倾斜角互补的两条直线,分别交椭圆于不同两点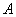 、
、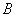 .
.
(Ⅰ)求证:直线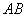 的斜率为一定值;
的斜率为一定值;
(Ⅱ)若直线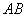 与
与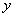 轴的交点
轴的交点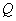 满足:
满足: ,求直线
,求直线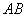 的方程;
的方程;
(Ⅲ)若在椭圆上存在关于直线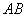 对称的两点,求直线
对称的两点,求直线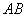 在
在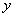 轴上截距的取值范围.
轴上截距的取值范围.
(Ⅰ)设椭圆方程为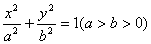 由
由
所以椭圆方程为 . …………………………………………………3分
. …………………………………………………3分
设直线 方程为
方程为 ,则直线
,则直线 的方程为
的方程为 ,
,
 ,
,
 .…………6分
.…………6分
另解:设直线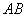 方程为
方程为 ,
,
由 消去
消去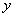 得,
得, ,
,
设 ,则
,则 ,
,
因为直线 的倾斜角互补,所以
的倾斜角互补,所以 ,
, ,
,
 ,
,
 ,
, ,解得
,解得 .
.
所以直线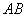 的斜率为一定值.
的斜率为一定值.
(参照上一解法评分)
(Ⅱ)由(Ⅰ)可设直线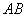 方程为
方程为 ,则
,则 ,设
,设 ,则
,则
由 得
得 .
.
由 ,
, ,
,
解得 ,所以直线
,所以直线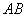 方程为
方程为 . …………………………………10分
. …………………………………10分
(Ⅲ)设 为椭圆上关于直线
为椭圆上关于直线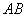 对称的两点,则
对称的两点,则
设 中点为
中点为 ,则
,则 ,
,
由 得
得 ,
,
又 ,所以
,所以
由点 在椭圆内知
在椭圆内知 ,,
,, ,解得
,解得 ,
,
即为直线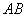 在
在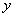 轴上截距的取值范围.
轴上截距的取值范围.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 为△
为△ 的三个内角,且其对边分别为
的三个内角,且其对边分别为 .若
.若 且
且 .
. ;
; ,三角形面积
,三角形面积 ,求
,求 、
、 的值.
的值. 中,
中, ,
, ,
, ,则
,则 .
.
 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦 中点
中点 在准线
在准线 上的射影为
上的射影为 的最大值为
的最大值为  B.
B. C.
C. D.
D.
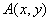 实施变换
实施变换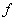 后,对应点为
后,对应点为 ,给出以下命题:
,给出以下命题: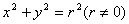 上任意一点实施变换
上任意一点实施变换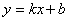 上每一点实施变换
上每一点实施变换 则
则 ;
;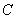 :
: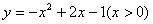 上每一点实施变换
上每一点实施变换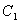 ,
,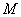 是曲线
是曲线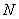 是曲线
是曲线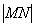 的最小值为
的最小值为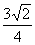 .
. A.1 B.
A.1 B. C.
C. D.
D.
 的展开式中,x的有理项共有_________项.
的展开式中,x的有理项共有_________项. ,则判断框中可填入
,则判断框中可填入
 B.
B. C.
C. D.
D.
 为第二象限角,且
为第二象限角,且 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.