题目内容
(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关
注:
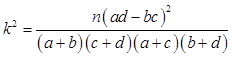
临界值表:
P(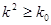 ) ) | 0.05 | 0.025 | 0.010 | 0.005 |
 | 3.841 | 5.024 | 6.635 | 7.879 |
解:(1)样本中满意的女游客为3名,样本中不满意的女游客为2名。
(2)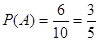 。
。
(3)有99%的把握认为:该景区游客性别与对景区的服务满意有关。
解析试题分析:(I)每个个体被抽取的概率为 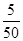 ,根据分层抽样,即可得样本中满意的女游客,样本中不满意的女游客的人数;
,根据分层抽样,即可得样本中满意的女游客,样本中不满意的女游客的人数;
(II)确定从这5名游客中随机选取两名的等可能事件的个数,其中事件A“选到满意与不满意的女游客各一名”包含6个基本事件,即可求得概率;
(III)由列联表,计算K2的值,根据P(K2>6.635)=0.010,即可得到结论.
解:(1)根据分层抽样可得:样本中满意的女游客为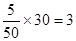 名,样本中不满意的女游客为
名,样本中不满意的女游客为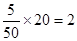 名。
名。
(2)记样本中对景区的服务满意的3名女游客分别为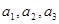 ,对景区的服务不满意的2名女游客分别为
,对景区的服务不满意的2名女游客分别为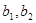 。从5名女游客中随机选取两名,共有10个基本事件,分别为:
。从5名女游客中随机选取两名,共有10个基本事件,分别为: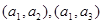 ,
,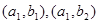 ,
,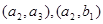 ,
,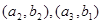 ,
,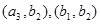 ;其中事件A:选到满意与不满意的女游客各一名包含了6个基本事件,分别为:
;其中事件A:选到满意与不满意的女游客各一名包含了6个基本事件,分别为: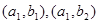 ,
,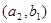
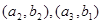 ,
,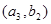
所以所求概率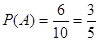 。
。
(3)假设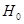 :该景区游客性别与对景区的服务满意无关,则
:该景区游客性别与对景区的服务满意无关,则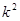 应该很小。
应该很小。
根据题目中列联表得: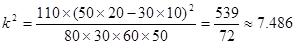
由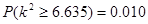 可知:有99%的把握认为:该景区游客性别与对景区的服务满意有关。
可知:有99%的把握认为:该景区游客性别与对景区的服务满意有关。
考点:本试题主要考查了分层抽样,考查等可能事件概率的求法,考查独立性检验知识,考查学生的计算能力,属于中档题.
点评:根据已知条件理解古典概型的概率中总的基本事件数从而求解概率的值,对于分层抽样的等概率抽样即为样本容量与总体的比值。

某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
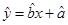 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。(相关公式:
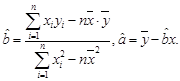 )
) (本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x | 2 | 4 | 5 | 6 | 8 |
| 销售额y | 30 | 40 | 60 | 50 | 70 |
(2)求y关于x的回归直线方程;
(3)预测当广告费支出为2(百万元)时,则这种产品的销售额为多少(百万元)
某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律:
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
下表是某地区的一种传染病与饮用水的调查表:
| | 得病 | 不得病 | 合计 |
| 干净水 | 52 | 466 | 518 |
| 不干净水 | 94 | 218 | 312 |
| 合计 | 146 | 684 | 830 |
参考数据:
 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

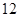 名男志愿者和
名男志愿者和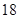 名女志愿者,调查发现,这
名女志愿者,调查发现,这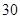 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )
 cm以上(包括
cm以上(包括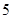 人,再从这
人,再从这 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?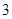 名志愿者,用
名志愿者,用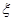 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出