题目内容
一袋中装有4n只红球和n只黑球(所有球的形状、大小都相同),每一次从袋中摸出两只球,且每次摸球后均放回袋中.现规定:摸出的两只球颜色不同则为中奖.设三次摸球恰有一次中奖的概率为P,则当n= 时,使得P最大.
【答案】分析:根据题意,设某一次中奖的概率为q,由古典概型公式和组合数公式可将q用n表示出来,进而由n次独立重复试验恰有k次发生的公式将p用q表示,分析可得q= 时,p最大;
时,p最大;
进而可得 =
= ,解可得n的值,即可得答案.
,解可得n的值,即可得答案.
解答:解:根据题意,设某一次中奖的概率为q,
在4n只红球和n只黑球任取2只有C5n2种取法,若摸出的两只球颜色不同即一红一黑有C4n1×Cn1种情况,
则q= =
=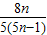 ;
;
若三次摸球恰有一次中奖,
则P=C31q•(1-q)2=3q(1-q)2= [(2q)(1-q)(1-q)],
[(2q)(1-q)(1-q)],
分析可得,当2q=1-q,即q= 时,p最大;
时,p最大;
若q= =
= ,解可得n=5;
,解可得n=5;
即n=5时,p最大;
故答案为5.
点评:本题考查排列、组合的应用,涉及基本不等式的运用,关键是熟练应用概率公式,求出两只球颜色不同的概率以及三次摸球恰有一次中奖的概率.
 时,p最大;
时,p最大;进而可得
 =
= ,解可得n的值,即可得答案.
,解可得n的值,即可得答案.解答:解:根据题意,设某一次中奖的概率为q,
在4n只红球和n只黑球任取2只有C5n2种取法,若摸出的两只球颜色不同即一红一黑有C4n1×Cn1种情况,
则q=
 =
=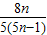 ;
;若三次摸球恰有一次中奖,
则P=C31q•(1-q)2=3q(1-q)2=
 [(2q)(1-q)(1-q)],
[(2q)(1-q)(1-q)],分析可得,当2q=1-q,即q=
 时,p最大;
时,p最大;若q=
 =
= ,解可得n=5;
,解可得n=5;即n=5时,p最大;
故答案为5.
点评:本题考查排列、组合的应用,涉及基本不等式的运用,关键是熟练应用概率公式,求出两只球颜色不同的概率以及三次摸球恰有一次中奖的概率.

练习册系列答案
相关题目