题目内容
设函数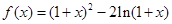 .
.
(I)求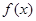 的单调区间;
的单调区间;
(II)当0<a<2时,求函数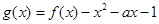 在区间
在区间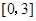 上的最小值.
上的最小值.
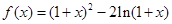 .
.(I)求
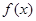 的单调区间;
的单调区间;(II)当0<a<2时,求函数
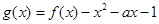 在区间
在区间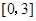 上的最小值.
上的最小值.(I)函数的单调递增区间为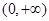 ,单调递减区间为
,单调递减区间为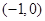 . (II)
. (II)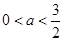 时,
时,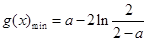 ;当
;当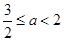 时,
时,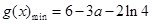 .
.
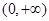 ,单调递减区间为
,单调递减区间为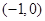 . (II)
. (II)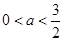 时,
时,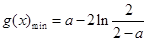 ;当
;当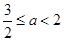 时,
时,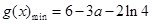 .
.第一问定义域为真数大于零,得到 .
.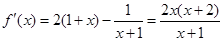 .
.
令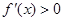 ,则
,则 ,所以
,所以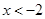 或
或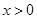 ,得到结论。
,得到结论。
第二问中,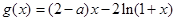 (
(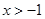 ).
).
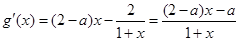 .
.
因为0<a<2,所以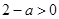 ,
,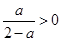 .令
.令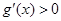 可得
可得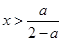 .
.
对参数讨论的得到最值。
所以函数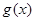 在
在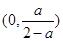 上为减函数,在
上为减函数,在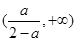 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
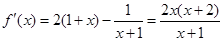 .
.
令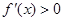 ,则
,则 ,所以
,所以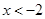 或
或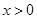 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以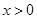 .
.
令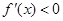 ,则
,则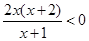 ,所以
,所以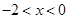 .
.
因为定义域为 ,所以
,所以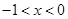 . ………………………5分
. ………………………5分
所以函数的单调递增区间为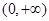 ,
,
单调递减区间为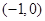 . ………………………7分
. ………………………7分
(II)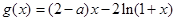 (
(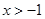 ).
).
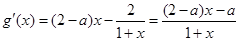 .
.
因为0<a<2,所以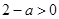 ,
,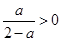 .令
.令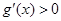 可得
可得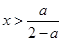 .…………9分
.…………9分
所以函数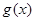 在
在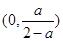 上为减函数,在
上为减函数,在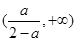 上为增函数.
上为增函数.
①当 ,即
,即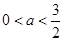 时,
时,
在区间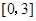 上,
上,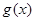 在
在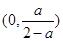 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以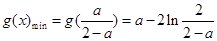 . ………………………10分
. ………………………10分
②当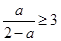 ,即
,即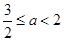 时,
时,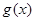 在区间
在区间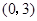 上为减函数.
上为减函数.
所以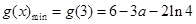 .
.
综上所述,当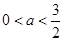 时,
时,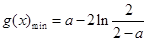 ;
;
当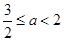 时,
时,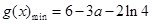
 .
.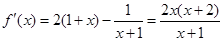 .
. 令
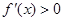 ,则
,则 ,所以
,所以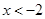 或
或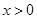 ,得到结论。
,得到结论。第二问中,
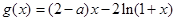 (
(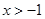 ).
).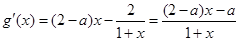 .
. 因为0<a<2,所以
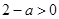 ,
,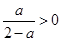 .令
.令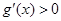 可得
可得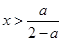 .
.对参数讨论的得到最值。
所以函数
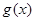 在
在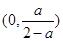 上为减函数,在
上为减函数,在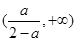 上为增函数.
上为增函数.(I)定义域为
 . ………………………1分
. ………………………1分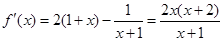 .
. 令
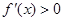 ,则
,则 ,所以
,所以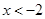 或
或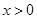 . ……………………3分
. ……………………3分 因为定义域为
 ,所以
,所以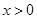 .
. 令
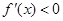 ,则
,则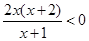 ,所以
,所以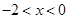 .
.因为定义域为
 ,所以
,所以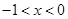 . ………………………5分
. ………………………5分所以函数的单调递增区间为
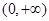 ,
,单调递减区间为
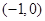 . ………………………7分
. ………………………7分(II)
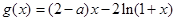 (
(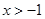 ).
).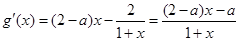 .
. 因为0<a<2,所以
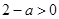 ,
,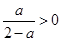 .令
.令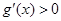 可得
可得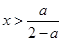 .…………9分
.…………9分所以函数
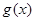 在
在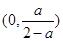 上为减函数,在
上为减函数,在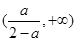 上为增函数.
上为增函数. ①当
 ,即
,即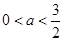 时,
时, 在区间
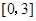 上,
上,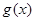 在
在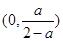 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.所以
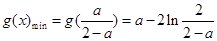 . ………………………10分
. ………………………10分 ②当
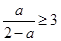 ,即
,即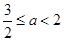 时,
时,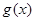 在区间
在区间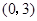 上为减函数.
上为减函数.所以
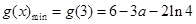 .
. 综上所述,当
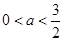 时,
时,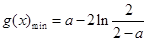 ;
;当
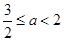 时,
时,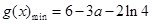

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
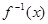 ,且对于任意的
,且对于任意的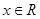 ,恒有f(x)+f(-x)=1,则
,恒有f(x)+f(-x)=1,则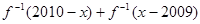 =( )
=( )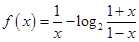 ,求函数的定义域,并判断它的奇偶性。
,求函数的定义域,并判断它的奇偶性。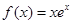 ,则( )
,则( ) 为
为 的极大值点
的极大值点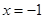 为
为 在区间
在区间 上的最大值是
上的最大值是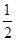


 的单调递减区间是 ;
的单调递减区间是 ; 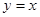 (
(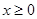 )和
)和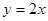 (
(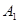 、
、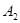 ,……,
,……,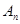 ,……,和点
,……,和点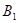 ,
,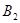 ,……,
,……,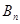 ……,其中
……,其中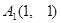 ,
,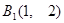 ,
,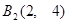 .且
.且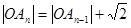 ,
, 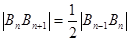
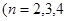 ……).
……).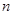 表示
表示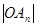 及点
及点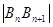 及点
及点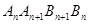 的面积关于
的面积关于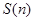 ,并求
,并求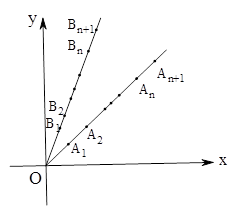
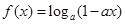 在区间
在区间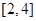 上是增函数,则实数
上是增函数,则实数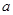 的取值范围是 。
的取值范围是 。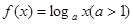 ,
,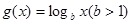 ,当
,当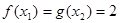 时,有
时,有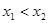 ,则
,则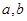 的大小关系是____________.
的大小关系是____________.