Question

（坐标系与参数方程选做题） 如图，AB是半径为1的圆的一条直径，C是此圆上任意一点，作射线AC，在AC上存在点P，使得AP•AC=1，以A为极点，射线AB为极轴建立极坐标系，则圆的方程为    、动点P的轨迹方程为    ．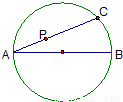

Answer 1

【答案】分析：由题意，设C（ρ，θ），则AC=ρ，∠CAB=θ，根据AB是半径为1的圆的一条直径，即可得圆的方程为ρ=2cosθ，P随着C的运动而运动，而C在圆上动，动点之间的关系是AP•AC=1，由此可得动点P方程．
解答：解：由题意，设C（ρ，θ），则AC=ρ，∠CAB=θ，
∵AB是半径为1的圆的一条直径
∴
∴圆的方程为ρ=2cosθ，
设C（ρ，θ），P（ρ′，θ），则ρ=2cosθ，
∵AP•AC=1
∴ρ′ρ=1
∴动点P方程为ρ′cosθ=．
即ρcosθ=．
故答案为：ρ=2cosθ；ρcosθ=．
点评：本题以圆为载体，考查圆的极坐标方程，考查代入法求轨迹方程，解题的关键是设点，列式．