题目内容
设锐角△ABC中,角ABC对边分别为a、b、c,且b=2asinB
(1)求角A的大小;(2)若a=2,求△ABC的面积的最大值.
(1)求角A的大小;(2)若a=2,求△ABC的面积的最大值.
(1)∵b=2asinB
∴sinB=2sinAsinB
得:sinA=
即A=
(2)∵a2=b2+c2-2bccosA=b2+c2-
bc≥2bc-
bc
∴bc≤
=4(2+
)
当且仅当b=c=
+
时取等号
S△ABC=
bcsinA≤
×4(2+
)×
=2+
即△ABC面积最大值为2+
(当且仅当b=c=
+
时取等号)
∴sinB=2sinAsinB
得:sinA=
| 1 |
| 2 |
| π |
| 6 |
(2)∵a2=b2+c2-2bccosA=b2+c2-
| 3 |
| 3 |
∴bc≤
| 4 | ||
2-
|
| 3 |
当且仅当b=c=
| 6 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
即△ABC面积最大值为2+
| 3 |
| 2 |
| 6 |

练习册系列答案
相关题目
 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、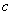 ,且
,且 。(1)求角
。(1)求角