题目内容
用长为a的铁丝弯成下部为矩形,上部为半圆形的框架(不含线段CD),若矩形底边长为2x.求(1)此框架围成的面积y关于x的函数解析式及定义域;
(2)当x为多少时,面积y取得最大值并求最大值.
分析:(1)首先根据已知表示出图中的长度,然后按照已知条件列出函数表达式,通过计算求出x的取值范围即为定义域;
(2)利用二次函数求最值的方法求解.
(2)利用二次函数求最值的方法求解.
解答: 解:(1)因为AB=2x,CD弧=πx,则AC=
解:(1)因为AB=2x,CD弧=πx,则AC=
(3分)
(2)当x=
时,y最大值=
=
(12分)
 解:(1)因为AB=2x,CD弧=πx,则AC=
解:(1)因为AB=2x,CD弧=πx,则AC=| a-2x-πx |
| 2 |
|
(2)当x=
| a |
| 4+π |
| -a2 | ||
4×[-(2+
|
| a2 |
| 8+2π |
点评:本题考查函数模型的选择与应用,通过对实际问题的分析,构造数学模型从而解决问题.需要对知识熟练的掌握并应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
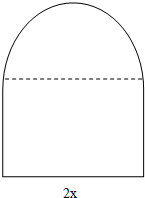 用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域.
用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域. 如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f (x),并写出它的定义域.
如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f (x),并写出它的定义域. 如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,此框架围成的面积为y,写出y关于x的函数,并写出它的定义域.
如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,此框架围成的面积为y,写出y关于x的函数,并写出它的定义域.