题目内容
如图,三棱柱ABC—A1B1C1中, 侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC中点。
(Ⅰ)求证:A1B∥平面AMC1;
(Ⅱ)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位
置;若不存在,请说明理由。
 |
解:(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
在三角形![]() 中,
中,![]() 是三角形
是三角形![]() 的中位线,
的中位线,
所以![]() ∥
∥![]() ,
,
又因![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() ∥平面
∥平面![]() .
.
(Ⅱ)(法一)设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]() 点到平面
点到平面![]() 的距离为
的距离为![]()
![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,
,
![]() 所以
所以![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() 因为
因为![]() ,
,
![]()
![]() 所以
所以![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
![]() ,
,![]() ,
,![]()
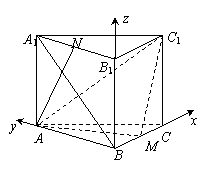
(法二)如图以![]() 所在的直线为
所在的直线为![]() 轴, 以
轴, 以![]() 所在
所在
的直线为![]() 轴, 以
轴, 以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 的长度为单位长度建立空间直角坐标系.
的长度为单位长度建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() .则有
.则有![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 令
令![]() ,得
,得![]() ,
,
∴![]() .
.
 (Ⅲ)假设直线
(Ⅲ)假设直线![]() 上存在点
上存在点![]() ,使
,使![]() 与
与![]() 成角为
成角为![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
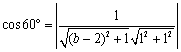
![]() ,
,
![]()
![]() 或
或![]() (舍去),
(舍去),
故![]() .所以在棱
.所以在棱![]() 上存在棱
上存在棱![]() 的中点
的中点![]() ,使
,使![]() 与
与![]() 成角
成角![]() .
.

练习册系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=