题目内容
【题目】已知函数![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(1)求![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为:![]() ,
,![]() ,证:
,证:![]() .
.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)由题得![]() ,令
,令![]() ,则函数
,则函数![]() 在定义域内有两个不同的极值点等价于
在定义域内有两个不同的极值点等价于![]() 在区间
在区间![]() 内至少有两个不同的零点,再利用导数得到
内至少有两个不同的零点,再利用导数得到![]() ,解不等式即得解;
,解不等式即得解;
(2)分析得到要证:![]() ,只需证明
,只需证明![]() ,即证
,即证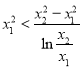 ,不妨设
,不妨设![]() ,即证
,即证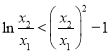 ,构造函数构造函数
,构造函数构造函数![]() ,其中
,其中![]() ,证明
,证明![]() 即得证.
即得证.
(1)由题意可知,![]() 的定义域为
的定义域为![]() ,
,
且![]() ,
,
令![]() ,
,
则函数![]() 在定义域内有两个不同的极值点等价于
在定义域内有两个不同的极值点等价于![]() 在区间
在区间![]() 内至少有两个不同的零点.
内至少有两个不同的零点.
由![]() 可知,
可知,
当![]() 时,
时,![]() 恒成立,即函数
恒成立,即函数![]() 在
在![]() 上单调,不符合题意,舍去.
上单调,不符合题意,舍去.
当![]() 时,由
时,由![]() 得,
得,![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
由![]() 得,
得,![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
故要满足题意,必有![]() ,解得
,解得![]() .
.
(2)证明:由(1)可知,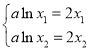 ,
,
故要证![]() ,
,
只需证明![]() ,
,
即证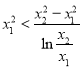 ,不妨设
,不妨设![]() ,即证
,即证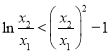 ,
,
构造函数![]() ,其中
,其中![]() ,
,
由![]() ,
,
所以函数![]() 在区间
在区间![]() 内单调递减,所以
内单调递减,所以![]() 得证.
得证.
即证![]() .
.

练习册系列答案
相关题目
【题目】在衡阳市“创全国文明城市”(简称“创文”)活动中,市教育局对本市A,B,C,D四所高中学校按各校人数分层抽样,随机抽查了200人,将调查情况进行整理后制成下表:
学校 | A | B | C | D |
抽查人数 | 10 | 15 | 100 | 75 |
“创文”活动中参与的人数 | 9 | 10 | 80 | 49 |
假设每名高中学生是否参与“创文”活动是相互独立的
(1)若本市共8000名高中学生,估计C学校参与“创文”活动的人数;
(2)在上表中从A,B两校没有参与“创文”活动的同学中随机抽取2人,求恰好A,B两校各有1人没有参与“创文”活动的概率;
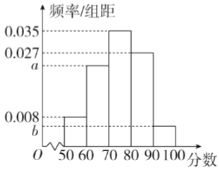
(3)在随机抽查的200名高中学生中,进行文明素养综合素质测评(满分为100分),得到如上的频率分布直方图,其中![]() .求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
.求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).