题目内容
已知椭圆C: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且经过点A(0,-1).
,且经过点A(0,-1).
(Ⅰ)求椭圆的方程;
(Ⅱ)如果过点(0, )的直线与椭圆交于M,N两点(M,N点与A点不重合),求
)的直线与椭圆交于M,N两点(M,N点与A点不重合),求 •
• 的值;当△AMN为等腰直角三角形时,求直线MN的方程.
的值;当△AMN为等腰直角三角形时,求直线MN的方程.
解:(I)因为椭圆经过点A(0,-1),所以b=1,
又e=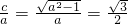 ,解得a=2,
,解得a=2,
所以椭圆的方程为 .
.
(II)①若过点(0, )的直线的斜率不存在,此时M,N两点中有一个点与A点重合,不满足题目条件,
)的直线的斜率不存在,此时M,N两点中有一个点与A点重合,不满足题目条件,
所以直线MN的斜率存在,设其斜率为k,则MN的方程为y=kx+ ,
,
把y=kx+ 代入椭圆方程得(1+4k2)x2+
代入椭圆方程得(1+4k2)x2+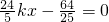 ,
,
设M(x1,y1),N(x2,y2),则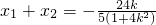 ,
,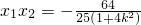 ,
,
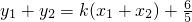 =
=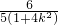 ,
,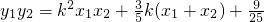 =
=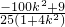 ,
,
因为A(0,-1),
所以 =(x1,y1+1)•(x2,y2+1)=x1x2+y1y2+(y1+y2)+1
=(x1,y1+1)•(x2,y2+1)=x1x2+y1y2+(y1+y2)+1
=-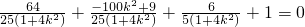 ;
;
②由①知:∠MAN=90°,如果△AMN为等腰直角三角形,设MN的中点为P,则AP⊥MN,且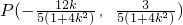 ,
,
若k=0,则P(0, ),显然满足AP⊥MN,此时直线MN的方程为y=
),显然满足AP⊥MN,此时直线MN的方程为y= ;
;
若k≠0,则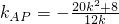 =-
=- ,解得k=
,解得k=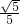 ,
,
所以直线MN的方程为y=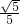 x+
x+ ,即
,即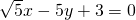 或
或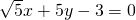 .
.
综上所述,直线MN的方程为y= 或
或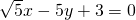 或
或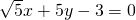 .
.
分析:(Ⅰ)由椭圆所过点A可求得b值,由离心率及a2=b2+c2可求得a值,从而得椭圆方程;
(Ⅱ)①易判断直线MN存在斜率,设M(x1,y1),N(x2,y2),MN的方程为y=kx+ ,代入椭圆方程消掉y得x的二次方程,由韦达定理、向量的数量积运算即可求得
,代入椭圆方程消掉y得x的二次方程,由韦达定理、向量的数量积运算即可求得 •
• 的值;②由①知:∠MAN=90°,设MN的中点为P,由△AMN为等腰直角三角形得AP⊥MN,由中点坐标公式可得P点坐标,分情况讨论:若k=0易求此时直线MN方程;若k≠0,则
的值;②由①知:∠MAN=90°,设MN的中点为P,由△AMN为等腰直角三角形得AP⊥MN,由中点坐标公式可得P点坐标,分情况讨论:若k=0易求此时直线MN方程;若k≠0,则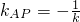 ,由斜率公式可得k的方程,解出得k,根据点斜式可求得直线MN方程,综上可得答案;
,由斜率公式可得k的方程,解出得k,根据点斜式可求得直线MN方程,综上可得答案;
点评:本题考查直线方程、椭圆方程及直线与椭圆位置关系,考查向量的数量积运算,考查分类讨论思想,考查学生综合运用知识分析解决问题的能力,综合性强,难度较大.
又e=
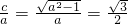 ,解得a=2,
,解得a=2,所以椭圆的方程为
 .
.(II)①若过点(0,
 )的直线的斜率不存在,此时M,N两点中有一个点与A点重合,不满足题目条件,
)的直线的斜率不存在,此时M,N两点中有一个点与A点重合,不满足题目条件,所以直线MN的斜率存在,设其斜率为k,则MN的方程为y=kx+
 ,
,把y=kx+
 代入椭圆方程得(1+4k2)x2+
代入椭圆方程得(1+4k2)x2+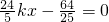 ,
,设M(x1,y1),N(x2,y2),则
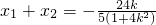 ,
,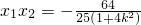 ,
,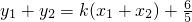 =
=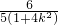 ,
,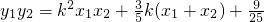 =
=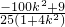 ,
,因为A(0,-1),
所以
 =(x1,y1+1)•(x2,y2+1)=x1x2+y1y2+(y1+y2)+1
=(x1,y1+1)•(x2,y2+1)=x1x2+y1y2+(y1+y2)+1=-
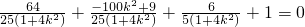 ;
;②由①知:∠MAN=90°,如果△AMN为等腰直角三角形,设MN的中点为P,则AP⊥MN,且
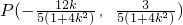 ,
,若k=0,则P(0,
 ),显然满足AP⊥MN,此时直线MN的方程为y=
),显然满足AP⊥MN,此时直线MN的方程为y= ;
;若k≠0,则
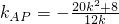 =-
=- ,解得k=
,解得k=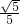 ,
,所以直线MN的方程为y=
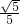 x+
x+ ,即
,即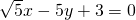 或
或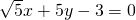 .
.综上所述,直线MN的方程为y=
 或
或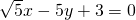 或
或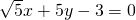 .
.分析:(Ⅰ)由椭圆所过点A可求得b值,由离心率及a2=b2+c2可求得a值,从而得椭圆方程;
(Ⅱ)①易判断直线MN存在斜率,设M(x1,y1),N(x2,y2),MN的方程为y=kx+
 ,代入椭圆方程消掉y得x的二次方程,由韦达定理、向量的数量积运算即可求得
,代入椭圆方程消掉y得x的二次方程,由韦达定理、向量的数量积运算即可求得 •
• 的值;②由①知:∠MAN=90°,设MN的中点为P,由△AMN为等腰直角三角形得AP⊥MN,由中点坐标公式可得P点坐标,分情况讨论:若k=0易求此时直线MN方程;若k≠0,则
的值;②由①知:∠MAN=90°,设MN的中点为P,由△AMN为等腰直角三角形得AP⊥MN,由中点坐标公式可得P点坐标,分情况讨论:若k=0易求此时直线MN方程;若k≠0,则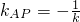 ,由斜率公式可得k的方程,解出得k,根据点斜式可求得直线MN方程,综上可得答案;
,由斜率公式可得k的方程,解出得k,根据点斜式可求得直线MN方程,综上可得答案;点评:本题考查直线方程、椭圆方程及直线与椭圆位置关系,考查向量的数量积运算,考查分类讨论思想,考查学生综合运用知识分析解决问题的能力,综合性强,难度较大.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为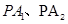 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.