Question

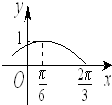（2013•长春一模）函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-

π

2

＜φ＜

π

2

）（x∈R）的部分图象如图所示．
（1）求函数y=f（x）的解析式；
（2）当x∈[-π，-

π

6

]时，求f（x）的取值范围．

Answer 1

分析：（1）由图象可求得A=1，由

T

4

=

π

2

可求得ω，f（x）过（

π

6

，1）点可求得φ，从而可求得函数y=f（x）的解析式；
（2）当x∈[-π，-

π

6

]时，可求得x+

π

3

的范围，利用正弦函数的单调性即可求得f（x）的取值范围．

解答：解：（1）由图象得A=1，

T

4

=

2π

3

-

π

6

=

π

2

，
∴T=2π，则ω=1；
将（

π

6

，1）代入得1=sin（

π

6

+φ），而-

π

2

＜φ＜

π

2

，
所以φ=

π

3

，因此函数f（x）=sin（x+

π

3

）；（6分）
（2）由于x∈[-π，-

π

6

]，
-

2π

3

≤x+

π

3

≤

π

6

，
所以-1≤sin（x+

π

3

）≤

1

2

，
所以f（x）的取值范围是[-1，

1

2

]．（ 12分）

点评：本小题主要考查三角函数解析式的求法与三角函数图象与性质的运用，以及三角函数的值域的有关知识，属于中档题．