题目内容
3.如图所示,用不同的五种颜色分别为A,B,C,D,E五部分着色,相邻部分不能用同一种颜色,但同一种颜色可以反复使用,也可不使用,则复合这些要求的不同着色的方法共有( )| A | B | |
| C | D | |
| E | ||
| A. | 500种 | B. | 520种 | C. | 540种 | D. | 560种 |
分析 由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,区域A有5种涂法,B有4种涂法,C有3种,D有3种涂法,E有3种涂法,根据乘法原理可得结论.
解答 解:先涂A,则A有5种涂法,再涂B,因为B与A相邻,所以B的颜色只要与A不同即可,有4种涂法,
同理C有3种涂法,D有3种涂法,E有3种涂法,
由分步乘法计数原理可知,复合这些要求的不同着色的方法共有为5×4×3×3×3=540,
故选:C.
点评 本题以实际问题为载体,考查计数原理的运用,关键搞清是分类,还是分步.

练习册系列答案
相关题目
14.设m,n是两条不同的直线,α,β是两个不同的平面,则下列叙述正确的是( )
| A. | 若α∥β,m∥α,n∥β,则m∥n | B. | 若α⊥β,m⊥α,n∥β,则m⊥n | ||
| C. | 若m∥α,n∥α,m∥β,n∥β,m⊥n,则α∥β | D. | 若m⊥α,n?β,m⊥n,则α⊥β |
18.已知函数f(x)=$\left\{\begin{array}{l}{sin(2x+\frac{π}{3})(x≥0)}\\{cos(ωx+φ)(x<0)}\end{array}\right.$(其中ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$).若对于任意的x均有f(x-$\frac{π}{6}$)=f($\frac{π}{3}$-x),则sin(ωφ)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
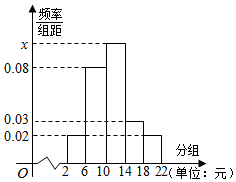 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.