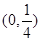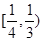题目内容
下列函数中既是奇函数又在区间 上单调递减的是( )
上单调递减的是( )
A. | B. |
C. | D. |
C
解析试题分析:根据定义可得: 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数; 是偶函数,只有
是偶函数,只有 与
与 是奇函数,由此可排除B、D.
是奇函数,由此可排除B、D.
而 在区间
在区间 上单调递增,也可排除,故选C
上单调递增,也可排除,故选C
考点:函数的单调性和奇偶性.

练习册系列答案
相关题目
函数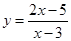 的值域是
的值域是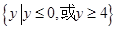 ,则此函数的定义域为( )
,则此函数的定义域为( )
A.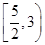 | B.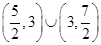 | C.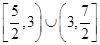 | D.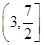 |
奇函数 在
在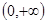 上为单调递减函数,且
上为单调递减函数,且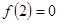 ,则不等式
,则不等式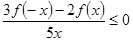 的解集为( )
的解集为( )
A.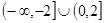 | B.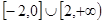 |
C.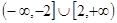 | D.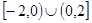 |
函数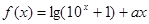 是偶函数,
是偶函数,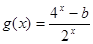 是奇函数,则
是奇函数,则 ( )
( )
| A.1 | B.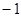 | C.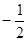 | D.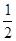 |
偶函数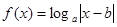 ,在
,在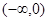 上单调递增,则
上单调递增,则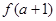 )与
)与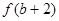 的大小关系是( )
的大小关系是( )
A. | B.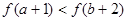 |
C.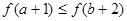 | D.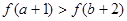 |
函数 的值域为( )
的值域为( )
A. | B. | C. | D.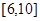 |
设函数 是定义在R上的奇函数,且当x
是定义在R上的奇函数,且当x 0时,
0时, 单调递减,若数列
单调递减,若数列 是等差数列,且
是等差数列,且 ,则
,则 的值 ( )
的值 ( )
| A.恒为负数 | B.恒为0 | C.恒为正数 | D.可正可负 |
 ,
, ,
, ,
, 的长度均为
的长度均为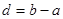 . 用
. 用 表示不超过
表示不超过 的最大整数,记
的最大整数,记 ,其中
,其中 .设
.设 ,
, ,若用
,若用 表示不等式
表示不等式 解集区间的长度,则当
解集区间的长度,则当 时,有 ( )
时,有 ( )



 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如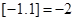 ,
, .若直线
.若直线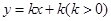 与函数
与函数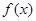 的图象恰好有3个不同的交点,则实数
的图象恰好有3个不同的交点,则实数 的取值范围是 ( )
的取值范围是 ( )