题目内容
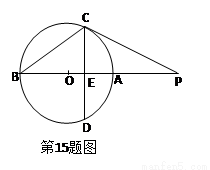
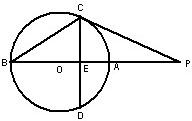如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则AB=________，sin∠P=________．
6 
分析：欲求AB的长度，需要建立起与其有关的方程，由题设条件，可以根据圆的切割线定理建立起关于PC，PA，PB的等式求出PA进而可求出AB，由于AB是直径，故半径已知，再连接OC，在直角三角形OCP中求出角P的正弦值即可．
解答：由图PC2=PA×PB，由于PC=4，PB=8，故可得PA=2，所以AB=6
由于割线PAB经过圆心O，故可知圆的直径是AB=6，故半径为3
连接OC，在直角三角形OPC中，可求得OP=
=5
故sin∠P=
=
故答案为：6；
点评：本题考点是与圆有关系的成比例线段，考查圆的切割线定理与直角三角形的中角的正弦的求法，本题是综合利用平面几何中的知识灵活变形解题，对做题者的思维深度要求较高．
分析：欲求AB的长度，需要建立起与其有关的方程，由题设条件，可以根据圆的切割线定理建立起关于PC，PA，PB的等式求出PA进而可求出AB，由于AB是直径，故半径已知，再连接OC，在直角三角形OCP中求出角P的正弦值即可．
解答：由图PC2=PA×PB，由于PC=4，PB=8，故可得PA=2，所以AB=6
由于割线PAB经过圆心O，故可知圆的直径是AB=6，故半径为3
连接OC，在直角三角形OPC中，可求得OP=
=5故sin∠P=
=故答案为：6；
点评：本题考点是与圆有关系的成比例线段，考查圆的切割线定理与直角三角形的中角的正弦的求法，本题是综合利用平面几何中的知识灵活变形解题，对做题者的思维深度要求较高．
练习册系列答案
相关题目
如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则AB=
（2012•红桥区一模）如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E．已知⊙O的半径为3，PA=2，则CD=
（2009•红桥区二模）（选做题）如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则CD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）