题目内容
已知f′(x)是函数f(x)=lnx+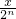 (x>0,n∈N*)的导函数,数列{an}满足1,an+1=
(x>0,n∈N*)的导函数,数列{an}满足1,an+1=
(1)求数列{an}的通项公式;
(2)若bn= ,Sn为数列{bn}的前n项和,求
,Sn为数列{bn}的前n项和,求 (Sn+bn)•
(Sn+bn)•
解(1)∵f(x)=lnx+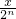 ,∴f′(x)=
,∴f′(x)= +
+ ,
,
结合an+1= ,可得
,可得 +
+ =
= ,∴
,∴ -
- =
= ,(3分)
,(3分)
因此 -
- =(
=( -
- )+(
)+( -
- )++(
)++( -
- )+(
)+( -
- )
)
= +
+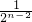 ++
++ +
+ =1-
=1- ,
,
所以 =2-
=2- ,即an=
,即an=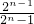 ,n∈N*.(6分)
,n∈N*.(6分)
(2)bn=(2n-1)•(2- )=(2n-1)•
)=(2n-1)• ,
,
Sn=1×1+3× +5×
+5× ++(2n-1)•
++(2n-1)• ,
,
 Sn=1×
Sn=1× +3×
+3× ++(2n-3)•
++(2n-3)• +(2n-1)•
+(2n-1)• ,
,
∴ Sn=1+2[
Sn=1+2[ +
+ ++
++ -(2n-1)•
-(2n-1)• ,(9分)
,(9分)
Sn=2+4•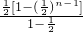 -(2n-1)
-(2n-1) =6-
=6-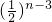 -(2n-1)•
-(2n-1)• =6-
=6-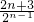 ,
,
∴ (sn+bn)=
(sn+bn)= (6-
(6-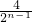 )=6.(12分)
)=6.(12分)
分析:(1)先求出函数的导数,然后代入an+1= ,整理得到,
,整理得到, -
- =
= ,然后求出
,然后求出 -
- ,即可求出通项公式.
,即可求出通项公式.
(2)首先求出数列{bn}通项公式,然后表示是出sn和 sn,再做差求得sn进而求出极限.
sn,再做差求得sn进而求出极限.
点评:本题考查了数列的求和、数列的极限等知识,对于等差数列和等比数列乘积形式的数列,一般采取错位相减的方法,属于中档题.
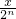 ,∴f′(x)=
,∴f′(x)= +
+ ,
,结合an+1=
 ,可得
,可得 +
+ =
= ,∴
,∴ -
- =
= ,(3分)
,(3分)因此
 -
- =(
=( -
- )+(
)+( -
- )++(
)++( -
- )+(
)+( -
- )
)=
 +
+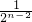 ++
++ +
+ =1-
=1- ,
,所以
 =2-
=2- ,即an=
,即an=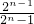 ,n∈N*.(6分)
,n∈N*.(6分)(2)bn=(2n-1)•(2-
 )=(2n-1)•
)=(2n-1)• ,
,Sn=1×1+3×
 +5×
+5× ++(2n-1)•
++(2n-1)• ,
, Sn=1×
Sn=1× +3×
+3× ++(2n-3)•
++(2n-3)• +(2n-1)•
+(2n-1)• ,
,∴
 Sn=1+2[
Sn=1+2[ +
+ ++
++ -(2n-1)•
-(2n-1)• ,(9分)
,(9分)Sn=2+4•
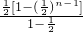 -(2n-1)
-(2n-1) =6-
=6-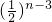 -(2n-1)•
-(2n-1)• =6-
=6-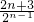 ,
,∴
 (sn+bn)=
(sn+bn)= (6-
(6-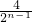 )=6.(12分)
)=6.(12分)分析:(1)先求出函数的导数,然后代入an+1=
 ,整理得到,
,整理得到, -
- =
= ,然后求出
,然后求出 -
- ,即可求出通项公式.
,即可求出通项公式.(2)首先求出数列{bn}通项公式,然后表示是出sn和
 sn,再做差求得sn进而求出极限.
sn,再做差求得sn进而求出极限.点评:本题考查了数列的求和、数列的极限等知识,对于等差数列和等比数列乘积形式的数列,一般采取错位相减的方法,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 已知f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是图中( )
已知f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是图中( )