题目内容
已知圆 ,直线
,直线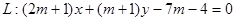
(1)求证:直线恒过定点
(2)判断直线被圆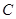 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。
 ,直线
,直线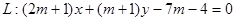
(1)求证:直线恒过定点
(2)判断直线被圆
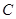 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。(1)见解析(2)当直线 垂直于
垂直于 时被截得弦长最短,此时
时被截得弦长最短,此时 ,最短弦长为
,最短弦长为
 垂直于
垂直于 时被截得弦长最短,此时
时被截得弦长最短,此时 ,最短弦长为
,最短弦长为
试题分析:(1)证明:直线
 的方程
的方程 ,
,经整理得
 , ……1分
, ……1分由
 的任意性
的任意性 , ……3分
, ……3分
 恒过定点
恒过定点 . ……5分
. ……5分(2)解:因为直线
 恒经过圆
恒经过圆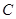 内一点
内一点 ,当直线
,当直线 垂直于
垂直于 时被截得弦长最短. ……7分
时被截得弦长最短. ……7分由
 、
、 ,直线
,直线 斜率
斜率 ,
,又直线
 与直线
与直线 垂直,
垂直,  直线
直线 的斜率为2,
的斜率为2,于是
 ,
, , ……9分
, ……9分最短弦长为
 , ……11分
, ……11分综上所述,当直线
 垂直于
垂直于 时被截得弦长最短,
时被截得弦长最短,此时
 ,最短弦长为
,最短弦长为 . ……12分
. ……12分点评:当直线与圆相交时,圆心到直线的距离、半弦长和半径组成一个直角三角形,这个直角三角形在解题时经常用到.

练习册系列答案
相关题目
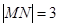 已知椭圆D:
已知椭圆D: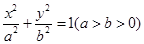 的焦距等于
的焦距等于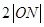 ,且过点
,且过点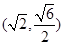

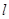 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.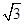 y-4=0相切,
y-4=0相切,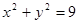 和
和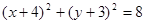 的交点的直线方程
的交点的直线方程  的两条渐近线均和圆
的两条渐近线均和圆 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆 的圆心,求该双曲线的方程。
的圆心,求该双曲线的方程。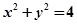 内点
内点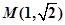 作圆的两条互相垂直的弦
作圆的两条互相垂直的弦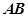 和
和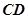 ,则
,则 的最大值为 .
的最大值为 . 

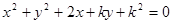 的面积最大时,圆心坐标是 ( )
的面积最大时,圆心坐标是 ( )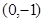
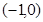
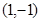
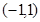
 ,则直线
,则直线 被圆
被圆 所截得的弦长为
所截得的弦长为 

