题目内容
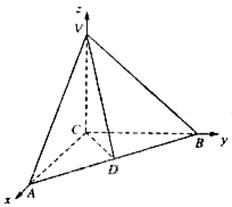
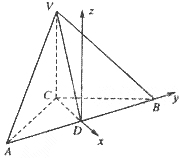
17.如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ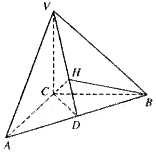
(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)试确定角θ的值,使得直线BC与平面VAB所成的角为![]() .
.
本小题主要考查线面关系,直线与平面所成角的有关知识,考查空间想象能力和推理运算能本,以及应用向量知识解决数学问题的能力.
解法1:(Ⅰ)∵AC=BC=a,∴△ACB是等腰三角形,又D是AB的中点,
∴CD⊥AB,又VC⊥底面ABC,∴VC⊥AB,于是AB⊥平面VCD,
又AB![]() 平面VAB,∴平面VAB⊥平面VCD.
平面VAB,∴平面VAB⊥平面VCD.
(Ⅱ)过C点C在平面VCD内作CH⊥VD于H,则由(Ⅰ)知CH⊥平面VAB.
连接BH,于是∠CBH就是直线BC与平面VAB所成的角.
依题意∠CBH=![]() ,所以
,所以

在Rt△CHD中,CH=![]() ;
;
在Rt△BHC中,CH=asin![]() ,
,
∴sinθ=![]() ∵0<θ<
∵0<θ<![]() ∴
∴![]()
故当![]() 时,直线BC与平面VAB所成的角为
时,直线BC与平面VAB所成的角为![]()
解法2:(Ⅰ)以CA、CB、CV所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直坐标系,则C(0,0,0),A(a,0,0),B(0,a,0),D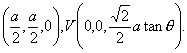
于是,![]()
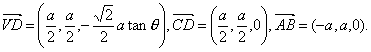
从而![]() ⊥CD.
⊥CD.
同理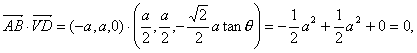 AB⊥VD.
AB⊥VD.
又CD∩VD=D,∴AB⊥平面VCD,
又AB![]() 平面VAB,
平面VAB,
∴平面VAB⊥平面VCD.
(Ⅱ)设平面VAB的一个法向量为n=(x,y,z),
则由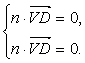
得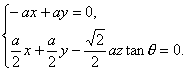
可取n=(1,1,![]() ),又
),又![]()
于是sin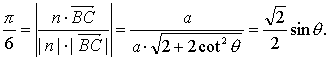
即sin=![]() ∵0<θ<
∵0<θ<![]() ∴
∴![]() .
.
故当θ=![]() 时,直线BC与平面VAB所成的角为
时,直线BC与平面VAB所成的角为![]()
解法3:(Ⅰ)以点D为原点,以DC、DB所在的直线分别在x轴、y轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(0,-![]() ),B(0,
),B(0, ![]() ),C(-
),C(-![]() ,0),
,0),
V(-![]() ,
,![]() ),于是
),于是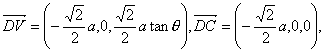
![]()
从而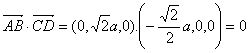
即AB⊥DC.
同理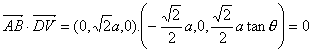
即AB⊥DV.
又DC∩DV=D,∴AB⊥平面VCD.
又AB![]() 平面VAB.
平面VAB.
∴平面VAB⊥平面VCD.
(Ⅱ)设平面VAB的一个法向量为n=(x·y·z),
则由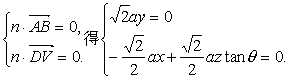
取n=(tanθ,0,1),又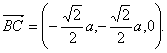
于是sin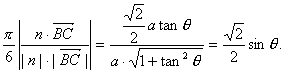
即sinθ=![]()
∵0<θ<![]() ∴
∴![]()
故当![]() 时,直线BC与平面VAB所成的角为
时,直线BC与平面VAB所成的角为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.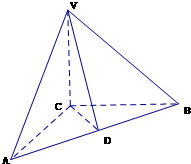 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.