题目内容
已知正实数x,y,z满足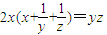 ,则
,则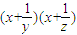 的最小值为 .
的最小值为 .
【答案】分析:先把已知中的式子展开,出现 ,代入
,代入 的展开式中,再用基本不等式就可求出最小值.
的展开式中,再用基本不等式就可求出最小值.
解答:解:∵x,y,z满足 ,
,
∴2x2+ +
+ =yz,
=yz,
又∵ =x2+
=x2+ +
+ +
+
∴ =
= +
+
∵x,y,z为正实数,∴ +
+ ≥2
≥2 =
=
即 ≥
≥ ,当且仅当
,当且仅当 =
= 时等号成立
时等号成立
∴ 的最小值为
的最小值为 .
.
故答案为
点评:本题主要考查了基本不等式的应用,做题时注意变形.
 ,代入
,代入 的展开式中,再用基本不等式就可求出最小值.
的展开式中,再用基本不等式就可求出最小值.解答:解:∵x,y,z满足
 ,
,∴2x2+
 +
+ =yz,
=yz,又∵
 =x2+
=x2+ +
+ +
+
∴
 =
= +
+
∵x,y,z为正实数,∴
 +
+ ≥2
≥2 =
=
即
 ≥
≥ ,当且仅当
,当且仅当 =
= 时等号成立
时等号成立∴
 的最小值为
的最小值为 .
.故答案为

点评:本题主要考查了基本不等式的应用,做题时注意变形.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
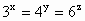 .求证:
.求证: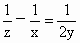 .
.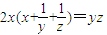 ,则
,则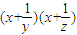 的最小值为 .
的最小值为 .