题目内容
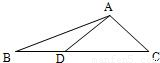
如图，在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上一点，DC=2BD，则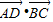
= ．
【答案】分析：法一：选定基向量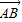
，
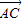将两向量
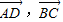，用基向量表示出来，再进行数量积运算，求出
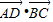的值．
法二：由余弦定理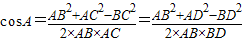得
，可得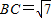
，
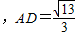又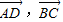
夹角大小为∠ADB，
，
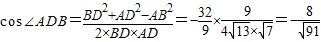所以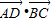
=
．
解答：解：法一：选定基向量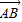
，
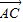，由图及题意得
，
=
∴
=（
）（
）=
+
=
=
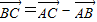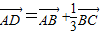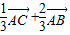
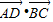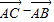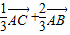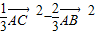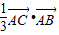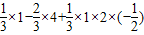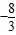
法二：由题意可得
∴
，
∵
，
∴
=
．
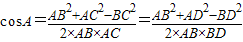
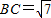
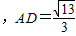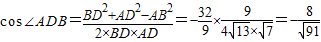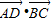故答案为：-
．
点评：本题主要考查余弦定理和向量数量积的应用．向量和三角函数的综合题是高考热点，要给予重视．
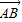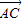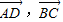，将两向量，用基向量表示出来，再进行数量积运算，求出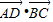的值．法二：由余弦定理得
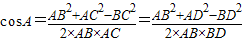，可得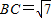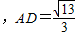，又
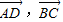夹角大小为∠ADB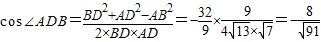，，所以
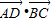=．解答：解：法一：选定基向量
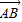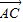，，由图及题意得，=∴
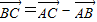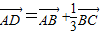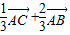
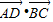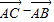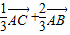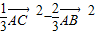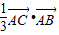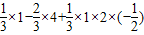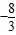
=（）（）=+==法二：由题意可得
∴
，∵
，∴
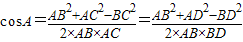
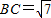
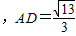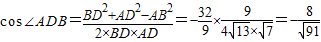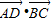=．故答案为：-
．点评：本题主要考查余弦定理和向量数量积的应用．向量和三角函数的综合题是高考热点，要给予重视．
练习册系列答案
智慧小复习系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知