题目内容
已知数列{an},{bn}满足bn=an+1-an,其中n=1,2,3,….(Ⅰ)若a1=1,bn=n,求数列{an}的通项公式;
(Ⅱ)若bn+1bn-1=bn(n≥2),且b1=1,b2=2.
(ⅰ)记cn=a6n-1(n≥1),求证:数列{cn}为等差数列;
(ⅱ)若数列
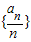 中任意一项的值均未在该数列中重复出现无数次.求a1应满足的条件.
中任意一项的值均未在该数列中重复出现无数次.求a1应满足的条件.
【答案】分析:(Ⅰ)根据数列的基本性质以及题中已知条件便可求出数列{an}的通项公式;
(Ⅱ)(ⅰ)先根据题中已知条件推导出bn+6=bn,然后求出cn+1-cn为定值,便可证明数列{cn}为等差数列;
(ⅱ)数列{a6n+i}均为以7为公差的等差数列,然后分别讨论当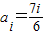 时和当
时和当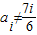 时,数列
时,数列 是否满足题中条件,便可求出a1应满足的条件.
是否满足题中条件,便可求出a1应满足的条件.
解答:解:(Ⅰ)当n≥2时,
有an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+…+bn-1(2分)
=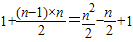 .(3分)
.(3分)
又因为a1=1也满足上式,
所以数列{an}的通项为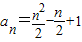 .(4分)
.(4分)
(Ⅱ)由题设知:bn>0,对任意的n∈N*有bn+2bn=bn+1,bn+1bn+3=bn+2得bn+3bn=1,
于是又bn+3bn+6=1,故bn+6=bn(5分)
∴b6n-5=b1=1,b6n-4=b2=2,b6n-3=b3=2,b6n-2=b4=1,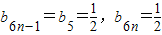
(ⅰ)cn+1-cn=a6n+5-a6n-1=b6n-1+b6n+b6n+1+b6n+2+b6n+3+b6n+4=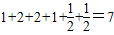 (n≥1),
(n≥1),
所以数列{cn}为等差数列.(7分)
(ⅱ)设dn=a6n+i(n≥0),(其中i为常数且i∈{1,2,3,4,5,6}),
所以dn+1-dn=a6n+6+i-a6n+i=b6n+i+b6n+i+1+b6n+i+2+b6n+i+3+b6n+i+4+b6n+i+5=7(n≥0)
所以数列{a6n+i}均为以7为公差的等差数列.(9分)
设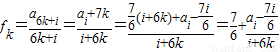 ,
,
(其中n=6k+i(k≥0),i为{1,2,3,4,5,6}中的一个常数),
当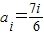 时,对任意的n=6k+i有
时,对任意的n=6k+i有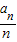 =
= ;(10分)
;(10分)
由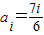 ,i∈{1,2,3,4,5,6}知
,i∈{1,2,3,4,5,6}知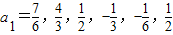 ;
;
此时 重复出现无数次.
重复出现无数次.
当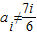 时,
时,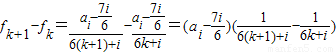 =
=
①若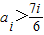 ,则对任意的k∈N有fk+1<fk,所以数列
,则对任意的k∈N有fk+1<fk,所以数列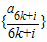 为单调减数列;
为单调减数列;
②若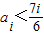 ,则对任意的k∈N有fk+1>fk,所以数列
,则对任意的k∈N有fk+1>fk,所以数列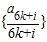 为单调增数列;
为单调增数列;
(12分)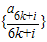 (i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,
(i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,
即数列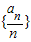 中任意一项的值最多出现六次.
中任意一项的值最多出现六次.
综上所述:当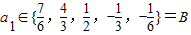 时,数列
时,数列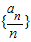 中必有某数重复出现无数次.
中必有某数重复出现无数次.
当a1∉B时,数列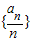 中任意一项的值均未在该数列中重复出现无数次.(14分)
中任意一项的值均未在该数列中重复出现无数次.(14分)
点评:本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,解题时分类讨论思想和转化思想的运用,属于中档题.
(Ⅱ)(ⅰ)先根据题中已知条件推导出bn+6=bn,然后求出cn+1-cn为定值,便可证明数列{cn}为等差数列;
(ⅱ)数列{a6n+i}均为以7为公差的等差数列,然后分别讨论当
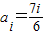 时和当
时和当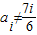 时,数列
时,数列 是否满足题中条件,便可求出a1应满足的条件.
是否满足题中条件,便可求出a1应满足的条件.解答:解:(Ⅰ)当n≥2时,
有an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+…+bn-1(2分)
=
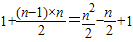 .(3分)
.(3分)又因为a1=1也满足上式,
所以数列{an}的通项为
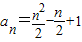 .(4分)
.(4分)(Ⅱ)由题设知:bn>0,对任意的n∈N*有bn+2bn=bn+1,bn+1bn+3=bn+2得bn+3bn=1,
于是又bn+3bn+6=1,故bn+6=bn(5分)
∴b6n-5=b1=1,b6n-4=b2=2,b6n-3=b3=2,b6n-2=b4=1,
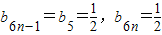
(ⅰ)cn+1-cn=a6n+5-a6n-1=b6n-1+b6n+b6n+1+b6n+2+b6n+3+b6n+4=
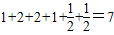 (n≥1),
(n≥1),所以数列{cn}为等差数列.(7分)
(ⅱ)设dn=a6n+i(n≥0),(其中i为常数且i∈{1,2,3,4,5,6}),
所以dn+1-dn=a6n+6+i-a6n+i=b6n+i+b6n+i+1+b6n+i+2+b6n+i+3+b6n+i+4+b6n+i+5=7(n≥0)
所以数列{a6n+i}均为以7为公差的等差数列.(9分)
设
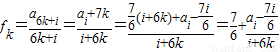 ,
,(其中n=6k+i(k≥0),i为{1,2,3,4,5,6}中的一个常数),
当
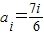 时,对任意的n=6k+i有
时,对任意的n=6k+i有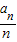 =
= ;(10分)
;(10分)由
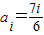 ,i∈{1,2,3,4,5,6}知
,i∈{1,2,3,4,5,6}知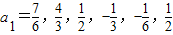 ;
;此时
 重复出现无数次.
重复出现无数次.当
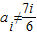 时,
时,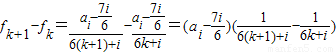 =
=
①若
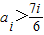 ,则对任意的k∈N有fk+1<fk,所以数列
,则对任意的k∈N有fk+1<fk,所以数列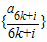 为单调减数列;
为单调减数列;②若
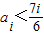 ,则对任意的k∈N有fk+1>fk,所以数列
,则对任意的k∈N有fk+1>fk,所以数列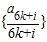 为单调增数列;
为单调增数列;(12分)
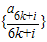 (i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,
(i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,即数列
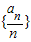 中任意一项的值最多出现六次.
中任意一项的值最多出现六次.综上所述:当
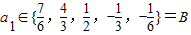 时,数列
时,数列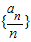 中必有某数重复出现无数次.
中必有某数重复出现无数次.当a1∉B时,数列
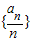 中任意一项的值均未在该数列中重复出现无数次.(14分)
中任意一项的值均未在该数列中重复出现无数次.(14分)点评:本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,解题时分类讨论思想和转化思想的运用,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目