题目内容
 把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=________.
把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=________.
70
分析:由题意可知,a63,7=(1+2+3+…+62)+(63-7)= =2010.
=2010.
解答:由题意可知,第一行有一个数,第二行有两个数,第三地有三个数,…,第62行有62个数,第63行有63个数,
∴a63,7=(1+2+3+…+62)+(63-7)=)= =2010.
=2010.
故m+n=63+7=70.
故答案为:70.
点评:本题借助于一个三角形数阵考查了数列的应用、数列的性质和应用,解题时要认真审题,仔细解答.是道基础题.
分析:由题意可知,a63,7=(1+2+3+…+62)+(63-7)=
 =2010.
=2010.解答:由题意可知,第一行有一个数,第二行有两个数,第三地有三个数,…,第62行有62个数,第63行有63个数,
∴a63,7=(1+2+3+…+62)+(63-7)=)=
 =2010.
=2010.故m+n=63+7=70.
故答案为:70.
点评:本题借助于一个三角形数阵考查了数列的应用、数列的性质和应用,解题时要认真审题,仔细解答.是道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

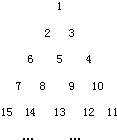 把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=
把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=
