题目内容
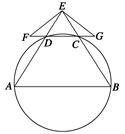
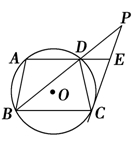
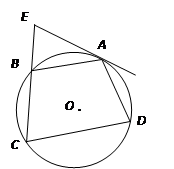
如图,已知⊙O是 的外接圆,
的外接圆,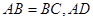 是
是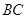 边上的高,
边上的高,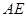 是⊙O的直径.
是⊙O的直径.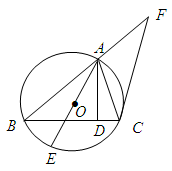
(1)求证: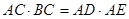 ;
;
(II)过点 作⊙O的切线交
作⊙O的切线交 的延长线于点
的延长线于点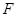 ,若
,若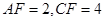 ,求
,求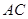 的长.
的长.
(I)详见解析;(II)3.
解析试题分析:(I)求证线段的比例关系,一般考虑证明三角形相似,AE是直径,直径所对的圆周角是直角,所以连接BE,证明 ∽
∽ ;(II)根据弦切线定理,可求得AB的长,在由
;(II)根据弦切线定理,可求得AB的长,在由 ∽
∽ 易求得AC的长.
易求得AC的长.
试题解析:(I)证明:连结 ,由题意知
,由题意知 为直角三角形.因为
为直角三角形.因为 所以
所以 ∽
∽ ,
,
则 ,则
,则 .又
.又 ,所以
,所以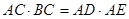 ,
,
(II)因为 是⊙O的切线,所以
是⊙O的切线,所以 ,
,
又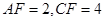 ,所以
,所以 .
.
因为 ,所以
,所以 ∽
∽
则 ,即
,即 .
.
考点:1、三角形相似的判定和性质 ; 2、圆的性质 ;3、弦切线定理的应用.

练习册系列答案
相关题目
 ,且AB是的
,且AB是的
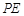 切⊙
切⊙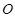 于点E,割线PBA交⊙
于点E,割线PBA交⊙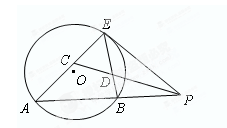
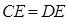 ; (Ⅱ)
; (Ⅱ)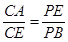 .
.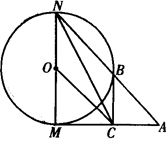
 是圆
是圆 的直径,
的直径,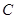 、
、 在圆
在圆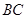 、
、 的延长线交直线
的延长线交直线 于点
于点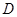 、
、 ,
, .求证:
.求证:
 .
.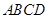 的外接圆为⊙
的外接圆为⊙ ,
,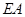 是⊙
是⊙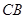 的延长线与
的延长线与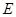 ,
,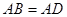 .
.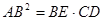 .
.
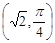 ,直线
,直线 的极坐标方程为
的极坐标方程为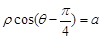 ,且点A在直线
,且点A在直线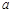 的值及直线
的值及直线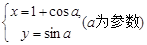 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.