题目内容
AB是过 右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是 .
右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是 .
【答案】分析:由方程易得焦点坐标,准线方程,取特殊位置AB垂直于x轴,可得坐标,进而可得A1B的方程,令y=0解x即可.
解答:解:由双曲线的方程可得a=4,b=3,故c= =5,故右焦点F(5,0)
=5,故右焦点F(5,0)
可取特殊情形:AB垂直于x轴,则A的横坐标是5,代入方程得到y= ,
,
右准线方程是x= =
= ,所以A1坐标是(
,所以A1坐标是( ,
, )B坐标是(5,
)B坐标是(5, )
)
直线A1B的斜率K= =-
=- ,
,
∴A1B的方程是:y+ =-
=- (x-2),
(x-2),
令y=0,得到x= ,即C坐标是(
,即C坐标是( ,0)
,0)
故答案为:( ,0)
,0)
点评:本题考查双曲线的简单性质,特殊位置是解决问题的关键,属中档题.
解答:解:由双曲线的方程可得a=4,b=3,故c=
 =5,故右焦点F(5,0)
=5,故右焦点F(5,0)可取特殊情形:AB垂直于x轴,则A的横坐标是5,代入方程得到y=
 ,
,右准线方程是x=
 =
= ,所以A1坐标是(
,所以A1坐标是( ,
, )B坐标是(5,
)B坐标是(5, )
)直线A1B的斜率K=
 =-
=- ,
,∴A1B的方程是:y+
 =-
=- (x-2),
(x-2),令y=0,得到x=
 ,即C坐标是(
,即C坐标是( ,0)
,0)故答案为:(
 ,0)
,0)点评:本题考查双曲线的简单性质,特殊位置是解决问题的关键,属中档题.

练习册系列答案
相关题目
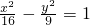 右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是________.
右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是________. 右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是 .
右焦点F的弦,过A作右准线的垂线AA1,A1为垂足,连接BA1交x轴于C点,则C的坐标是 .