题目内容
设正项等比数列{an}的首项a1=(1)求{an}的通项;
(2)求{nSn}的前n项和Tn.
解:(1)由210S30-(210+1)S20+S10=0,得210(S30-S20)=S20-S10,
即210(a21+a22+…+a30)=a11+a12+…+a20,
可得210·q10(a11+a12+…+a20)=S11+a12+…+a20.
因为an>0,所以210q10=1,解得q=![]() ,因而an=a1qn-1=
,因而an=a1qn-1=![]() ,n=1,2,….
,n=1,2,….
(2)因为{an}是首项a1=![]() ,公比q=
,公比q=![]() 的等比数列,故
的等比数列,故
Sn=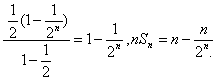 .
.
则数列{nSn}的前n项和Tn=(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() ),
),
![]() =
=![]() (1+2+…+n)-(
(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() +
+![]() .
.
前两式相减,得
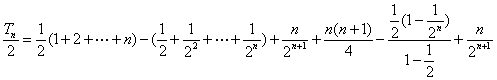 ,?
,?
即Tn=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目