题目内容
设等比数列{an}的前n项和为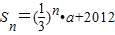 ,则a= .
,则a= .
【答案】分析:根据an=Sn-Sn-1求得数列的通项公式,进而求得a1,根据a1=S1求得a
解答:解:∵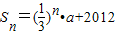 ,
,
∴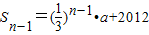 ,(n≥2,n∈N+),
,(n≥2,n∈N+),
∴an=Sn-Sn-1=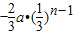 ,
,
当n=1时,a1=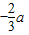
又a1=S1=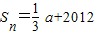 ,
,
∴a=-2012
故答案为:-2012
点评:本题考查的知识点是等比数列的前n项和,其中根据an=Sn-Sn-1求得数列的通项公式,是解答的关键.
解答:解:∵
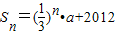 ,
,∴
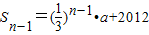 ,(n≥2,n∈N+),
,(n≥2,n∈N+),∴an=Sn-Sn-1=
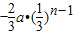 ,
,当n=1时,a1=
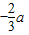
又a1=S1=
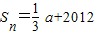 ,
,∴a=-2012
故答案为:-2012
点评:本题考查的知识点是等比数列的前n项和,其中根据an=Sn-Sn-1求得数列的通项公式,是解答的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |