题目内容
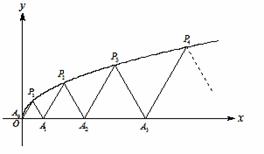
如图,![]() 、
、![]() 、…、
、…、![]() (
(![]() )是曲线
)是曲线![]() :
:![]() (
(![]() )上的
)上的![]() 个点,点
个点,点![]() (
(![]() )在
)在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 是正三角形(
是正三角形(![]() 是坐标原点).
是坐标原点).
(Ⅰ)写出![]() 、
、![]() 、
、![]() ;
;
(Ⅱ)求出点![]() (
(![]() )的横坐标
)的横坐标![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,若对任意的正整数
,若对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)![]() ,
,![]() ,
,![]() ;
;
(Ⅱ)依题意,得![]() ,
,![]() ,由此及
,由此及![]() 得
得
![]() ,
,
即![]() .
.
由(Ⅰ)可猜想:![]() (
(![]() ).
).
下面用数学归纳法予以证明:
(1)当![]() 时,命题显然成立;
时,命题显然成立;
(2)假定当![]() 时命题成立,即有
时命题成立,即有![]() ,则当
,则当![]() 时,由归纳假设及
时,由归纳假设及
![]()
得![]() ,即
,即
![]() ,
,
解之得![]() (
(![]() 不合题意,舍去),
不合题意,舍去),
即当![]() 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立.
(Ⅲ)![]()
![]()
 .
.
令![]() (
(![]() ),则
),则![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
故当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,即当
,即当![]() 时,
时,![]() .
.
![]() (
(![]() ,
,![]() )
)
![]() ,即
,即![]() (
(![]() )
)
![]() .
.
解之得,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
 (理科)如图所示的几何体底面ABC是直角三角形,∠CAB=90°,AC=4,AB=4,DA,EC,FB均垂直于底面ABC,且CE=3,BF=1,AD=2,点G为棱EF上的一点,且
(理科)如图所示的几何体底面ABC是直角三角形,∠CAB=90°,AC=4,AB=4,DA,EC,FB均垂直于底面ABC,且CE=3,BF=1,AD=2,点G为棱EF上的一点,且 如图,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心)P-ABCD的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于( )
如图,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心)P-ABCD的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于( ) 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点. 一个多面体是由正方体割去两个三棱锥得到的,其正视图、侧视图、府视图均是边长为2的正方形,如图所示,该多面体的表面积是( )
一个多面体是由正方体割去两个三棱锥得到的,其正视图、侧视图、府视图均是边长为2的正方形,如图所示,该多面体的表面积是( ) 已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.
已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.