Question

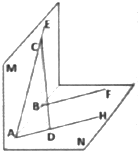直二面角M-AB-N中，AE、BF分别在平面M和N内，AE、BF和棱AB的夹角分别是α和β，且AB=a，求证：AE和BF的距离d=

a

1+cot2α+cot2β

．

Answer 1

分析：过A点作BF的平行线AD，则AE和BF的距离d即为B点到平面ACD的距离，令AC=AD=a，连接BC，BD，CD，利用等积法，可求出d值．

解答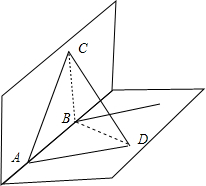：证明：过A点作BF的平行线AD，令AC=AD=a，连接BC，BD，CD
则AE和BF的距离d即为B点到平面ACD的距离
∵AE、BF和棱AB的夹角分别是α和β，且AB=a，
∴S_△ABD=

1

2

sinβ•a²，
又∵二面角M-AB-N为直二面角，故C到△ABD的距离h=sinα•a
故三棱锥的体积V=

1

3

S_△ABD•h=

1

6

sinαsinβ•a³•a³
由三余弦定理，可得cos∠CAD=cosα•cosβ
故S_△ACD=

1

2

sin∠CAD•a²=

1

2

1-cos2α•cos2β

•a²
故d=

V

1 3 S△ACD

=

1 6 •sinα•sinβ•a3

1 6 1-cos2α•cos2β •a2

=

a

1-cos2α•cos2β sinα•sinβ

=

a

1-cos2α•cos2β sin2α•sin2β

=

a

sin2α•sin2β+sin2α•cos 2β+cos2α•sin2β sin2α•sin2β

=

a

1+cot2α+cot2β

即d=

a

1+cot2α+cot2β

点评：本题考查的知识点是异面直线的距离，其中将异面直线的距离问题，转化为点到平面之间的距离是解答的关键．