题目内容
当0≤x≤2时，不等式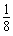
(2t-t)2≤x2-3x+2≤3-t2恒成立，试求t的取值范围．
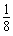(2t-t)2≤x2-3x+2≤3-t2恒成立，试求t的取值范围． 解：令y=x2-3x+2，0≤x≤2，
∵y=x2-3x+2=(x-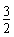
)2-
，
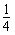∴y在0≤x≤2上取得最小值为-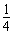
，最大值为2，
若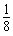
(2t-t)2≤x2-3x+2≤3-t2在0≤x≤2上恒成立，
则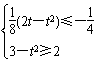
，即
，
∴
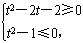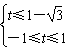或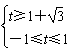
，
∴t的取值范围为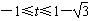
。
∵y=x2-3x+2=(x-
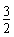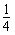)2-， ∴y在0≤x≤2上取得最小值为-
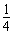，最大值为2，若
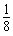(2t-t)2≤x2-3x+2≤3-t2在0≤x≤2上恒成立，则
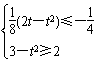，即，∴
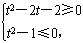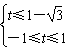或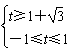，∴t的取值范围为
。
练习册系列答案
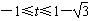名校课堂系列答案
相关题目
已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，0＜φ＜